题目内容
已知平面 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:
(1)  ∥
∥

 (2)
(2) 
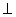


 ∥
∥
(3)  ∥
∥


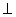
 (4)
(4) 

 ∥
∥
其中正确的是( )
| A.(1)与(2) | B.(3)与(4) | C.(1)与(3) | D.(2)与(4) |
C
解析试题分析:解:对于①l⊥α,α∥β,m?β⇒l⊥m正确;对于②l⊥α,m?β,α⊥β⇒l∥m;l与m也可能相交或者异面;对于③l∥m,l⊥α⇒m⊥α,又因为m?β则α⊥β正确;对于④l⊥m,l⊥α则m可能在平面α内,也可能不在平面α内,所以不能得出α∥β;综上所述①③正确,故选C
考点:平面与平面之间的位置关系
点评:本题考查平面与平面之间的位置关系,考查空间想像能力及组织材料判断面面间位置关系的能力,属于基本题型.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知 、
、 、
、 是三条不同的直线,
是三条不同的直线, 、
、 、
、 是三个不同的平面,给出以下命题:
是三个不同的平面,给出以下命题:
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;③若
;③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 .
.
其中正确命题的序号是( )
| A.②④ | B.②③ | C.③④ | D.①③ |
设 为两条直线,
为两条直线,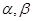 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( )
A.若 且 且 ,则 ,则 | B.若 且 且 ,则 ,则 |
C.若 , , 则 则 | D.若 则 则 |
对于两条不相交的空间直线 和
和 ,必定存在平面
,必定存在平面 ,使得 ( )
,使得 ( )
A. | B. | C. | D. |
已知m,n是两条不重合的直线, 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若m
 ,m
,m
 ,则
,则 ∥
∥ ; ②若
; ②若

 ,
,

 则
则 ∥
∥
③若m// ,n //
,n // ,m//n 则
,m//n 则 //
// ④若m
④若m
 ,m//
,m// ,则
,则


其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
在空间四边形 中,
中, 分别为
分别为 的中点,若
的中点,若 则
则 与
与 所成的角为
所成的角为
A. | B. | C. | D. |
 ,则这个二面角的大小为( )
,则这个二面角的大小为( )








 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=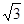 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 

