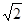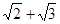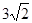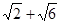题目内容
在空间四边形 中,
中, 分别为
分别为 的中点,若
的中点,若 则
则 与
与 所成的角为
所成的角为
A. | B. | C. | D. |
D
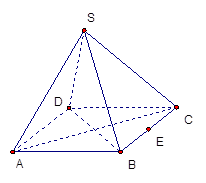
解析试题分析:根据题意,作图
根据题意,
 分别为
分别为 的中点
的中点
然后H,G是AD,BC的中点,HF= =EF,HEGF是平行四边形,HE=
=EF,HEGF是平行四边形,HE=
看⊿HEF:∵AB⊥EF,∴HF⊥EF.HF=1,HE=2,.∴∠HEF=30°.而HE//CD,
∴EF与CD所成角为30°,故选D.
考点:异面直线所成的角
点评:通过平移法来得到异面直线的所成的角是解题的关键,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知平面 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:
(1)  ∥
∥

 (2)
(2) 
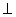


 ∥
∥
(3)  ∥
∥


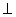
 (4)
(4) 

 ∥
∥
其中正确的是( )
| A.(1)与(2) | B.(3)与(4) | C.(1)与(3) | D.(2)与(4) |
空间四边形ABCD中,若 ,则
,则 与
与 所成角为( )
所成角为( )
A. | B. | C. | D. |
已知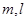 是两条不同的直线,
是两条不同的直线,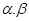 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若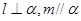 ,则
,则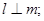 ②若
②若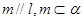 则
则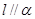 ;
;
③若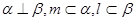 则
则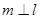 ; ④若
; ④若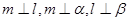 则
则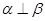 ;
;
其中正确命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设 ,
, 是两条不同的直线,
是两条不同的直线,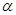 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
正方体 中,下列结论错误的是
中,下列结论错误的是
A. ∥平面 ∥平面 | B. 平面 平面 |
C. | D.异面直线 与 与 所成的角是45º 所成的角是45º |
设m、n是两条不同的直线,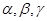 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若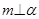 ,
,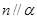 ,则
,则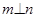 ②若
②若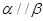 ,
,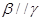 ,
,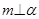 ,则
,则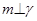
③若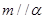 ,
,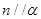 ,则
,则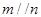 ④若
④若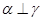 ,
, 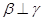 ,则
,则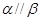
其中正确命题的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①②③④ |
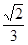
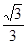
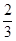
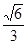
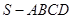 的底面边长为2,高为2,
的底面边长为2,高为2,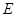 为边
为边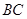 的中点,动点
的中点,动点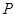 在表面上运动,并且总保持
在表面上运动,并且总保持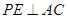 ,则动点
,则动点