题目内容
正方体ABCD-A1B1C1D1中,M、N分别为棱AB,DD1中点,则异面直线A1M与C1N所成的角是( )
| A.0 | B. | C. | D. |
D
解析试题分析:根据题意,由于正方体的各个面是正方形,那么可知在正方形内,取 的中点E,则连接
的中点E,则连接 ,则可知异面直线A1M与C1N所成的角是就是直线A1M与
,则可知异面直线A1M与C1N所成的角是就是直线A1M与 所成的角,在正方形内,根据相似的性质可知,A1M与
所成的角,在正方形内,根据相似的性质可知,A1M与 垂直,故选D.
垂直,故选D.
考点:异面直线所成的角
点评:解决的关键是将直线平移到一个平面内,然后借助于平面的性质来判定,属于基础题。

练习册系列答案
相关题目
点 到直线
到直线 :
: 的距离的最大值为( )
的距离的最大值为( )
A. | B. | C. | D. |
两条异面直线所成角的范围是( )
A. | B. | C. | D. |
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |
已知平面 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:
(1)  ∥
∥

 (2)
(2) 
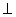


 ∥
∥
(3)  ∥
∥


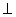
 (4)
(4) 

 ∥
∥
其中正确的是( )
| A.(1)与(2) | B.(3)与(4) | C.(1)与(3) | D.(2)与(4) |
从正方体的八个顶点中任取四个点连线,在能构成的一对异面直线中,其所成的角的度数不可能是
| A.30° | B.45° | C.60° | D.90° |
设 ,
, 是两条不同的直线,
是两条不同的直线,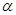 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,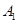 在底面
在底面 上的射影为
上的射影为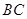 的中点D,则异面直线AD与
的中点D,则异面直线AD与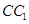 所成的角的余弦值为( )
所成的角的余弦值为( )

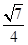
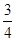
 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )