题目内容
学校在高二开设了当代战争风云、投资理财、汽车模拟驾驶与保养、硬笔书法共4门选修课,每个学生必须且只需选修1门选修课,对于该年级的甲、乙、丙3名学生.
(Ⅰ)求这3名学生选择的选修课互不相同的概率;
(Ⅱ)求恰有2门选修课没有被这3名学生选择的概率;
(Ⅲ)求投资理财选修课被这3名学生选择的人数的数学期望.
(Ⅰ)求这3名学生选择的选修课互不相同的概率;
(Ⅱ)求恰有2门选修课没有被这3名学生选择的概率;
(Ⅲ)求投资理财选修课被这3名学生选择的人数的数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)这3名学生选择的选修课的基本事件总数n=43,这3名学生选择的选修课互不相同包含的基本事件个数m=
,由此能求出这3名学生选择的选修课互不相同的概率.
(Ⅱ)这3名学生选择的选修课的基本事件总数n=43,恰有2门选修课没有被这3名学生选择包含的基本事件个数m=
(23-2),由此能求出恰有2门选修课没有被这3名学生选择的概率.
(Ⅲ)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3,分别求出相应的概率,由此能求出投资理财选修课被这3名学生选择的人数的数学期望.
| A | 3 4 |
(Ⅱ)这3名学生选择的选修课的基本事件总数n=43,恰有2门选修课没有被这3名学生选择包含的基本事件个数m=
| C | 2 4 |
(Ⅲ)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3,分别求出相应的概率,由此能求出投资理财选修课被这3名学生选择的人数的数学期望.
解答:
解:(Ⅰ)这3名学生选择的选修课的基本事件总数n=43,
这3名学生选择的选修课互不相同包含的基本事件个数m=
,
∴这3名学生选择的选修课互不相同的概率p1=
=
.
(Ⅱ)这3名学生选择的选修课的基本事件总数n=43,
恰有2门选修课没有被这3名学生选择包含的基本事件个数m=
(23-2),
∴恰有2门选修课没有被这3名学生选择的概率p2=
=
.
(Ⅲ)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3,
P(ζ=0)=
=
,
P(ζ=1)=
=
,
P(ζ=2)=
=
,
P(ζ=3)=
=
.(11分)
X的分布列为
Eξ=0×
+1×
+2×
+3×
=
.
这3名学生选择的选修课互不相同包含的基本事件个数m=
| A | 3 4 |
∴这3名学生选择的选修课互不相同的概率p1=
| ||
| 43 |
| 3 |
| 8 |
(Ⅱ)这3名学生选择的选修课的基本事件总数n=43,
恰有2门选修课没有被这3名学生选择包含的基本事件个数m=
| C | 2 4 |
∴恰有2门选修课没有被这3名学生选择的概率p2=
| ||
| 43 |
| 9 |
| 16 |
(Ⅲ)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3,
P(ζ=0)=
| 33 |
| 43 |
| 27 |
| 64 |
P(ζ=1)=
| ||
| 43 |
| 27 |
| 64 |
P(ζ=2)=
3•
| ||
| 43 |
| 9 |
| 64 |
P(ζ=3)=
| ||
| 43 |
| 1 |
| 64 |
X的分布列为
| ζ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
函数F(x)=
t(t-4)dt在[-1,5]上( )
| ∫ | x 0 |
| A、有最大值0,无最小值 | ||
B、有最大值0,最小值-
| ||
C、有最小值-
| ||
| D、既无最大值也无最小值 |
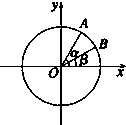 如图,在平面直角坐标系xOy中,以OX轴的非负半轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
如图,在平面直角坐标系xOy中,以OX轴的非负半轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为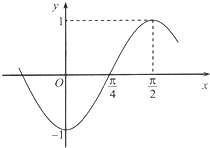 已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示. 如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.
如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.