题目内容
18.已知数列{an}满足an+1+2=$\frac{3{a}_{n}+4}{2{a}_{n}+3}$,且a1=1,设bn=$\frac{{a}_{n}+1}{{2}_{\;}}$,则数列{bn•bn+1}的前50项和为$\frac{50}{201}$.分析 数列{an}满足an+1+2=$\frac{3{a}_{n}+4}{2{a}_{n}+3}$,可得$\frac{1}{{a}_{n+1}+1}$=$\frac{2{a}_{n}+3}{{a}_{n}+1}$,化为:$\frac{1}{{a}_{n+1}+1}$-$\frac{1}{{a}_{n}+1}$=2,利用“裂项求和”方法即可得出.
解答 解:∵数列{an}满足an+1+2=$\frac{3{a}_{n}+4}{2{a}_{n}+3}$,
∴$\frac{1}{{a}_{n+1}+1}$=$\frac{2{a}_{n}+3}{{a}_{n}+1}$,化为:$\frac{1}{{a}_{n+1}+1}$-$\frac{1}{{a}_{n}+1}$=2,
∴数列{$\frac{1}{{a}_{n}+1}$}是以$\frac{1}{2}$为首项,2为公差的等差数列,
则$\frac{1}{{a}_{n}+1}$=2n-$\frac{3}{2}$,∴bn=$\frac{{a}_{n}+1}{2}$=$\frac{1}{4n-3}$,
则bn•bn+1=$\frac{1}{(4n-3)(4n+1)}$=$\frac{1}{4}({\frac{1}{4n-3}-\frac{1}{4n+1}})$,
∴${b_1}•{b_2}+…+{b_{50}}•{b_{51}}=\frac{1}{4}({1-\frac{1}{201}})=\frac{50}{201}$.
故答案为:$\frac{50}{201}$.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.等比数列{an}的前n项和为Sn,已知S1,2S2,3S3成等差数列,则{an}的公比为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
3.如图所示的程序框图,若f(x)=logax,g(x)=lnx,输入x=2016,则输出的h(x)=( )
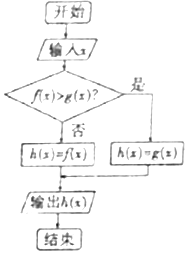

| A. | 2016 | B. | 2017 | C. | loga2016 | D. | loga2017 |