题目内容
已知f(x)=1n(x+1)-ax(a∈R)
(1)求y=f(x)的单调区间;
(2)当a=1时,求f(x)在定义域上的最大值.
(1)求y=f(x)的单调区间;
(2)当a=1时,求f(x)在定义域上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知得f(x)的定义域为{x|x>-1},f′(x)=
-a,由此利用分类讨论思想能求出f(x)的单调区间.
(Ⅱ)当a=1时,f(x)=ln(x+1)-x,由此利用导数性质能求出f(x)在定义域上的最大值.
| 1 |
| x+1 |
(Ⅱ)当a=1时,f(x)=ln(x+1)-x,由此利用导数性质能求出f(x)在定义域上的最大值.
解答:
解:(Ⅰ)∵f(x)=1n(x+1)-ax,
∴f(x)的定义域为{x|x>-1},f′(x)=
-a,
当a=0时,∵f′(x)=
>0,∴f(x)的单调增区间为(-1,+∞);
当a<0时,∵f′(x)=
-a>0,∴f(x)的单调增区间为(-1,+∞);
当a>0时,由f(x)′=
-a>0,得x<
-1,
∴f(x)的单调递增区间为(-1,
),
由f′(x)<0,得x>
-1,∴f(x)的减区间为(
,+∞).
(Ⅱ)当a=1时,f(x)=ln(x+1)-x,
由(Ⅰ)知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴x=0时,f(x)在定义域上取最大值f(0)=0.
∴f(x)的定义域为{x|x>-1},f′(x)=
| 1 |
| x+1 |
当a=0时,∵f′(x)=
| 1 |
| x+1 |
当a<0时,∵f′(x)=
| 1 |
| x+1 |
当a>0时,由f(x)′=
| 1 |
| x+1 |
| 1 |
| a |
∴f(x)的单调递增区间为(-1,
| 1-a |
| a |
由f′(x)<0,得x>
| 1 |
| a |
| 1-a |
| a |
(Ⅱ)当a=1时,f(x)=ln(x+1)-x,
由(Ⅰ)知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴x=0时,f(x)在定义域上取最大值f(0)=0.
点评:本题考查函数的单调区间和最小值的求法,解题时要认真审题,注意分类讨论思想和导数性质的合理运用.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
已知集合A={x|22x-1≤
},B={y|log
y≥
},则∁RA∩B=( )
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |
| A、∅ | ||||
B、(0,
| ||||
C、(0,
| ||||
D、(-
|
 如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点.
如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点.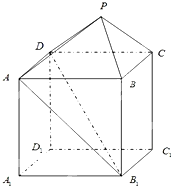 如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=
如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=