题目内容
等差数列{an}中,a4+a6-a11=3,a12-a5=2,记Sn=a1+a2+…+an,则S11= .
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列的性质已知两式相加可得a6=5,再由求和公式可得S11=11a6,代值计算可得.
解答:
解:∵等差数列{an}中,a4+a6-a11=3,a12-a5=2,
∴两式相加可得(a4+a12)-(a11+a5)+a6=5,
由等差数列的性质可得a4+a12=a11+a5,∴a6=5
∴S11=
=
=11a6=55
故答案为:55
∴两式相加可得(a4+a12)-(a11+a5)+a6=5,
由等差数列的性质可得a4+a12=a11+a5,∴a6=5
∴S11=
| 11(a1+a11) |
| 2 |
| 11×2a6 |
| 2 |
故答案为:55
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知是R上的奇函数,且f(x+2)=-f(x),当0≤x≤1时,则f(x)=x,则f(7.5)=( )
| A、0.5 | B、1.5 |
| C、-0.5 | D、-1.5 |
已知全集U=R,A={x|x>0},B={x|x>1},则A∩∁UB( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|0≤x<1} |
| D、{x|0≤x≤1} |
不等式组
表示的平面区域是( )
|
A、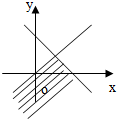 |
B、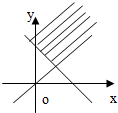 |
C、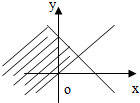 |
D、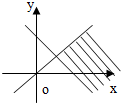 |
 如图,函数f(x)的图象是曲线OAB,其中点O(0,0),A(1,2),B(3,1),则
如图,函数f(x)的图象是曲线OAB,其中点O(0,0),A(1,2),B(3,1),则