题目内容
17．已知a＜b，则在下列的一段推理过程中，错误的推理步骤有③④．（填上所有错误步骤的序号）
分析 逐步判断各推理步骤是否符合不等式的性质即可．
解答 解：步骤①在不等式两边同时加a，不等式仍成立，故步骤①正确；
步骤②在不等式的两边同时减2b，不等式仍成立，故步骤②正确；
步骤③在不等式两边同时乘（a-b），由于a＜b，故a-b＜0，不等号需改变方向，故步骤③错误；
步骤④在不等式两边同时除以（a-b）2，由于（a-b）2＞0，不等号方向不变，故步骤④错误．
故答案为：③④．
点评 本题考查了不等式的性质，进行简单的推理证明，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
15．已知随机变量ξ～B（n，p），且E（ξ）=12，D（ξ）=2.4，则n与p的值分别是（ ）
| A． | 15，$\frac{4}{5}$ | B． | 18，$\frac{2}{3}$ | C． | 20，$\frac{3}{5}$ | D． | 24，$\frac{1}{2}$ |
8．若m∈（4，7），则直线y=kx+k与圆x2+y2+mx+4=0至少有一个交点的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{3}$ |
棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，求图中三角形（正四面体的截面）的面积．
6．
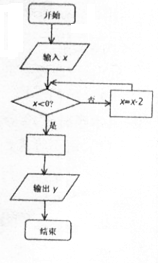如图是一个算法程序框图，当输入的x的值为4时，输出的结果恰好是$\frac{1}{4}$，则空白处的关系式可以是（ ）
如图是一个算法程序框图，当输入的x的值为4时，输出的结果恰好是$\frac{1}{4}$，则空白处的关系式可以是（ ）| A． | y=2-x | B． | y=2x | C． | y=x${\;}^{-\frac{1}{2}}$ | D． | y=x${\;}^{\frac{1}{2}}$ |