题目内容

9．等比数列{an}的前n项和为Sn，若a2=2，a5=16，则S1+S2+…+Sn=2n+1-n-2．

分析 求出等比数列的公比，求出Sn，然后求解S1+S2+…+Sn即可．

解答 解：等比数列{an}的前n项和为Sn，若a2=2，a5=16，可得q3=$\frac{16}{2}$=8，q=2，
∴a1=1．Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1．
∴S1+S2+…+Sn=（21+22+23+…+2n）-n
=$\frac{2（1-{2}^{n}）}{1-2}$-n
=2n+1-n-2．
故答案为：2n+1-n-2．

点评 本题考查数列求和，等比数列的性质的应用，考查计算能力．

练习册系列答案
相关题目
7．已知圆C：x2+y2+Dx+Ey+3=0，圆C关于直线x+y-1=0对称，圆心在第二象限，半径为$\sqrt{2}$．
（1）求圆C的方程；
（2）已知不过原点的直线l与圆C相切，且在x轴、y轴上的截距相等，求直线l的方程；
（3）已知点A（-1，1），若点B在圆C上运动，P是AB的中点，求动点P的轨迹方程．
20．已知函数f（x）=$\sqrt{2}$cosx（sinx+cosx）．
（Ⅰ）若0＜α＜$\frac{π}{2}$，且sinα=$\frac{\sqrt{2}}{2}$，求f（α）的值；
（Ⅱ）求函数f（x）的最小正周期及单调递增区间．
17．已知a＜b，则在下列的一段推理过程中，错误的推理步骤有③④．（填上所有错误步骤的序号）
4．如图，在△ABC中，$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$，记$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$，则$\overrightarrow{ED}$=$\frac{\overrightarrow{a}-\overrightarrow{b}}{3}$（用$\overrightarrow{a}$，$\overrightarrow{b}$表示）．
14．已知圆O：x2+y2=2，圆M：（x-a）2+（y-a+4）2=1．若圆M上存在点P，过点P作圆O的两条切线，切点为A、B，使得四边形PAOB为正方形，则实数a的取值范围为[$2-\frac{\sqrt{2}}{2}，2+\frac{\sqrt{2}}{2}$]．
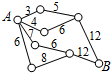1．如图，小圆圈表示网络结点，结点之间的连线表示它们之间有网线连接，连线标注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点A向结点B发送信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为（　　）
A．19B．20C．24D．26
18．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知cosB=$\frac{2\sqrt{5}}{5}$，tanC=$\frac{1}{3}$．
（Ⅰ）求tanA；    
（Ⅱ）若c=1，求△ABC的面积．
19．已知函数f（x）=$\left\{{\begin{array}{l}{{x^2}-1，x＜1}\\{-{{log}_2}x，x≥1}\end{array}}$．
（1）在图中画出该函数的图象；
（2）写出函数f（x）的值域、单调区间及零点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网