题目内容
10.已知定义域为R的函数f(x)满足:①x∈(0,1]时,f(x)=2x-1;②对任意x∈R均有f(x+1)=2f(x).定义[x]是不超过x的最大整数,如[-0.1]=-1,[1.2]=1,g(x)=$\frac{[x]}{x}$.(1)求f(2)的值;
(2)求函数f(x)在(1,2]上的解析式;
(3)设不等式f(x)≤8在区间(-∞,a]上恒成立时a的最大值为M,且函数h(x)=g(x)-t(x∈(0,M])仅有三个零点,求实数t的取值范围.
分析 (1)令x=1代入f(x+1)=2f(x),再计算出f(1)即可;
(2)根据f(x+1)=2f(x)及x∈(0,1]时,f(x)=2x-1,可以得出x∈(1,2]时,f(x)=2x-2;
(3)分别求出x∈(2,3],(3,4],(4,5]的函数解析式,根据f(x)≤8得出M=4,再画出g(x)在(0,4]内的函数图象,运用数形结合求出t的取值范围;
解答 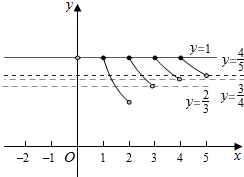 解:(1)根据题意,因为,x∈(0,1]时,f(x)=2x-1,
解:(1)根据题意,因为,x∈(0,1]时,f(x)=2x-1,
且对任意x∈R均有f(x+1)=2f(x),
所以,令x=1代入上式得,
f(2)=2f(1)=2(21-1)=2;
(2)因为,f(x+1)=2f(x),
所以,f(x)=2f(x-1),
当x∈(1,2]时,f(x)=2f(x-1)=2(2x-1-1)=2x-2,
即x∈(1,2]时,f(x)=2x-2;
(3)由(2)知,x∈(1,2]时,f(x)=2x-2≤2恒成立,
当x∈(2,3]时,f(x)=2f(x-1)=2(2x-1-2)=2x-4≤4恒成立,
当x∈(3,4]时,f(x)=2f(x-1)=2(2x-1-4)=2x-8≤8恒成立,
当x∈(4,5]时,f(x)=2f(x-1)=2(2x-1-8)=2x-16≤16恒成立,
由于不等式f(x)≤8在区间(-∞,a]上恒成立时a的最大值为M,所以M=4,
当x∈(0,4]时,g(x)=$\frac{[x]}{x}$的图象如右图所示:
显然,方程g(x)=1在(0,4]内有四个根,g(x)=$\frac{3}{4}$在(0,4]内有两个根,
因此,要使h(x)=g(x)-t有三个零点,则t∈($\frac{3}{4}$,1),
即实数t的取值范围为:($\frac{3}{4}$,1).
点评 本题主要考查了函数解析式的求法以及函数值的确定,函数零点的判断,涉及抽象函数的图象和性质以及数形结合的解题思想,属于难题.

| A. | {a|a>1} | B. | {a|a<-2或a>1} | C. | {a|-2<a<1} | D. | {a|a<-2} |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
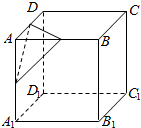 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )| A. | 此多面体的表面积为$\frac{47}{8}$a2 | B. | 体对角线AC1垂直于截面 | ||
| C. | 截面平行于平面CB1D1 | D. | 有10个顶点 |
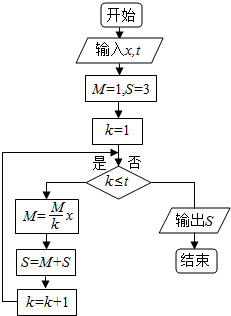
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
