题目内容

3．函数f（x）=x2+2x+1的单调递增区间是（　　）
A．[-1，+∞）B．[1，+∞）C．（-∞，-1]D．（-∞，1]

分析 判断函数的对称轴以及开口方向，然后求解即可．

解答 解：函数f（x）=x2+2x+1的开口向上，对称轴为x=-1，函数f（x）=x2+2x+1的单调递增区间是[-1，+∞）．
故选：A．

点评 本题考查二次函数的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
13．已知函数$f（x）=sin（2ωx-\frac{π}{6}）$将其图象向左平移$\frac{π}{4}$个单位得到函数g（x）图象，且函数g（x）图象关于y轴对称，若ω是使变换成立的最小正数，则ω=$\frac{4}{3}$．
14．若函数f（x）=2sin（πx+φ）+1（0＜φ＜π）是偶函数，则φ=$\frac{π}{2}$．
11．函数f（x）的图象如图所示，则下列关系正确的是（　　）
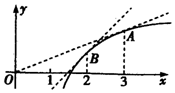
A．0＜f'（2）＜f'（3）＜f（3）-f（2）B．0＜f'（2）＜f（3）-f（2）＜f'（3）C．0＜f'（3）＜f（3）-f（2）＜f'（2）D．0＜f（3）-f（2）＜f'（2）-f'（3）
18．老张身高176cm，他爷爷、父亲、儿子的身高分别是173cm、170cm和182cm，因儿子的身高与父亲的身高有关，父亲的身高用x表示，儿子的身高用y来表示．
（1）完成答题卡中的表格；
（2）用回归分析的方法得到的回归方程为$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$，则预计老张的孙子的身高为多少？
8．设函数f（x）=sinxcosx-$\sqrt{3}$cos（x+π）cosx（x∈R）．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=f（x）的图象按$\overrightarrow{b}$=（$\frac{π}{4}$，$\frac{\sqrt{3}}{2}$）平移后得到函数y=g（x）的图象，求y=g（x）在[0，$\frac{π}{4}$]上的最大值．
15．已知函数y=$\frac{2}{3}$x3-2x2+3，
（1）求在点（1，$\frac{5}{3}$）处的切线方程，
（2）求函数在[-1，3]的最值．
12．已知等比数列{an}的公比q=2，其前4项和S4=60，则a3=16．
13．i为虚数单位，则${（{\frac{1+i}{1-i}}）^{2013}}$=（　　）
A．iB．-iC．1D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网