题目内容
3.如图(1),五边形ABCDE中,ED=EA,AB∥CD,CD=2AB,∠EDC=150°.如图(2),将△EAD沿AD折到△PAD的位置,得到四棱锥P-ABCD.点M为线段PC的中点,且BM⊥平面PCD.
(1)求证:平面PAD⊥平面PCD;
(2)若直线PC与AB所成角的正切值为$\frac{1}{2}$,设AB=1,求四棱锥P-ABCD的体积.
分析 (1)取PD的中点N,连接AN,MN,由三角形中位线定理可得及已知可得四边形ABMN为平行四边形,得AN∥BM,在由已知BM⊥平面PCD,可得AN⊥平面PCD,由面面垂直的判定可得平面PAD⊥平面PCD;
(2)取AD的中点O,连接PO,由AN⊥平面PCD,可得AN⊥PD,AN⊥CD.再由已知可得△PAD为等边三角形,得到CD⊥AD,则平面PAD⊥平面ABCD.再由线面垂直的性质可得PO是锥P-ABCD的高.由已知直线PC与AB所成角的正切值为$\frac{1}{2}$,AB=1求得CD=2,PA=AD=AB=1,再由棱锥体积公式求得四棱锥P-ABCD的体积.
解答 (1)证明:取PD的中点N,连接AN,MN,则$MN∥CD,MN=\frac{1}{2}CD$,
又$AB∥CD,AB=\frac{1}{2}CD$,∴MN∥AB,MN=AB,
则四边形ABMN为平行四边形,∴AN∥BM,
又BM⊥平面PCD,∴AN⊥平面PCD,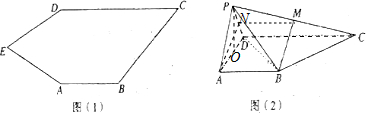
∵AN⊆面PCD,
∴平面PAD⊥平面PCD;
(2)解:取AD的中点O,连接PO,
∵AN⊥平面PCD,
∴AN⊥PD,AN⊥CD.
由ED=EA,即PD=PA及N为PD的中点,可得△PAD为等边三角形,
∴∠PDA=60°,
又∠EDC=150°,∴∠CDA=90°,则CD⊥AD,
∴CD⊥平面PAD,CD?平面ABCD,
∴平面PAD⊥平面ABCD.
∵PO⊥AD,面PAD∩面ABCD=AD,PO?面PAD,
∴PO⊥面ABCD,
PO是锥P-ABCD的高.
∵AB∥CD,∴∠PCD为直线PC与AB所成的角,
由(1)可得∠PDC=90°,∴$tan∠PCD=\frac{PD}{CD}=\frac{1}{2}$,得CD=2PD,
由AB=1,可知CD=2,PA=AD=AB=1,
∴PO=$\sqrt{1-(\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$,
${S}_{ABCD}=\frac{1}{2}(1+2)×2=3$.
则${V}_{P-ABCD}=\frac{1}{3}•{S}_{ABCD}•PO$=$\frac{1}{3}×3×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,是中档题.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | 6π | B. | 36π | C. | 7π | D. | 49π |
| A. | 2016 | B. | 1008 | C. | 504 | D. | 2017 |
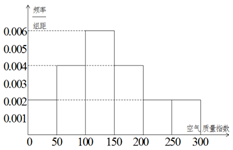 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度 污染 | 4级中度 污染 | 5级重度 污染 | 6级严重污染 |
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在(0,150]的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{7}{32}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中点.