题目内容
13. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中点.(1)求证:PC∥平面EBD;
(2)过点D作DF⊥PC,垂足为F,求证:平面DEF⊥平面PCB.
分析 (1)设AC交BD于O,连接EO,则由中位线定理可得PC∥OE,故而PC∥平面EBD;
(2)先证BC⊥平面PDC得出BC⊥DF,结合DF⊥PC得出DF⊥平面PBC,故而平面DEF⊥平面PCB.
解答 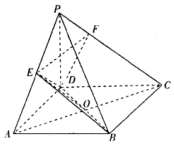 证明:(1)设AC交BD于O,连接EO,
证明:(1)设AC交BD于O,连接EO,
在△PAC中,∵E是PA中点,O是AC中点.
∴EO∥PC.
又PC?平面EBD,EO?平面EBD,
∴PC∥平面EBD.
(2)∵PD⊥平面ABCD,BC?平面ABCD.
∴PD⊥BC.
又BC⊥DC,DC∩PD=D,PD?平面PDC,DC?平面PDC,
∴BC⊥平面PDC.又DF?平面PDC,
∴BC⊥DF.
又DF⊥PC,BC∩PC=C,BC?平面PCB,PC?平面PCB,
∴DF⊥平面PCB,
∵DF?平面DEF,
∴平面DEF⊥平面PCB.
点评 本题考查了线面平行,线面垂直的判定,面面垂直的判定,属于基础题.

练习册系列答案
相关题目
3.某班有男生30人,女生20人,按分层抽样方法从班级中选出5人负责校园开放日的接待工作.现从这5人中随机选取2人,至少有1名男生的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
8.命题“?x∈R,使得n≥x2”的否定形式是( )
| A. | ?x∈R,使得n<x2 | B. | ?x∈R,使得n≥x2 | C. | ?x∈R,使得n<x2 | D. | ?x∈R,使得n≤x2 |
18.若a<b<0,则下列不等式不能成立的是( )
| A. | |a|>|b| | B. | a2>ab | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | $\frac{1}{a-b}>\frac{1}{a}$ |
5.曲线y=2x3-x2+1在点(1,2)处的切线方程为( )
| A. | y=3x-4 | B. | y=4x-2 | C. | y=-4x+3 | D. | y=4x-5 |
2.下列函数中,既是奇函数,又在区间(0,+∞) 上单调递增的函数为( )
| A. | y=x2-x | B. | y=x+2sin x | C. | y=x3+x | D. | y=tan x |
