题目内容
14.函数f(x)为定义在R上的奇函数,且在(0,+∞)上为增函数,f(3)=0,则不等式f(2x-1)≥0的解为( )| A. | $[{-1,\frac{1}{2}})∪[{2,+∞})$ | B. | $[{-1,\frac{1}{2}}]∪({2,+∞})$ | C. | [2,+∞) | D. | $[{-1,\frac{1}{2}})$ |
分析 根据函数的奇偶性和单调性之间的关系,画出函数f(x)的草图,即可得到不等式的解集.
解答 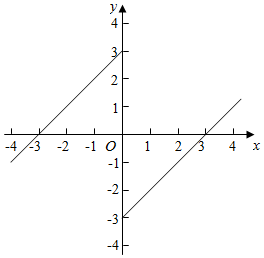 解:∵奇函数f(x)在(0,+∞)上为增函数,f(3)=0,
解:∵奇函数f(x)在(0,+∞)上为增函数,f(3)=0,
∴函数f(x)在(-∞,0)上为增函数,且f(-3)=-f(3)=0,
作出函数f(x)的草图:
如图:由不等式f(2x-1)≥0得2x-1≥3或2x-1=0或-3≤2x-1<0,
即x≥2或x=$\frac{1}{2}$或-1≤x<$\frac{1}{2}$,
综上x≥2或-1≤x≤$\frac{1}{2}$,
即不等式的解集为$[{-1,\frac{1}{2}}]∪({2,+∞})$,
故选:B
点评 本题主要考查不等式的解法,利用函数的奇偶性和单调性之间的关系是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.已知双曲线E的渐近线方程为3x±4y=0,且E的右焦点为(5,0),过双曲线E中心的直线与双曲线E交于A,B两点,在双曲线E上取一点C,直线AC,BC的斜率分别为k1、k2,则k1k2等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{9}{16}$ | D. | $\frac{16}{25}$ |
8.若函数f(x)=sin(ωx+φ)+$\sqrt{3}$cos(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)为偶函数,且在区间($\frac{3π}{4}$,π)上单调递增,则ω的最小值为( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{3}{4}$ |
9.若中心在原点,对称轴为坐标轴的双曲线的渐近线方程为y=±$\sqrt{2}$x,则该双曲线的离心率为( )
| A. | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{6}}{2}$或3 | C. | $\sqrt{3}$ | D. | 3 |
6.已知F是双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1的右焦点,点P的坐标为(3,1),点A在双曲线上,则|AP|+|AF|的最小值为( )
| A. | $\sqrt{37}$+4 | B. | $\sqrt{37}$-4 | C. | $\sqrt{37}$-2$\sqrt{5}$ | D. | $\sqrt{37}$+2$\sqrt{5}$ |
4.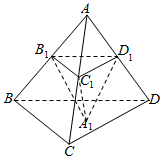 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )| A. | 当x=$\frac{2}{3}$时,函数f(x)取到最大值 | |
| B. | 函数f(x)在($\frac{1}{2}$,1)上是减函数 | |
| C. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| D. | 存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$(其中VA-BCD为四面体ABCD的体积) |
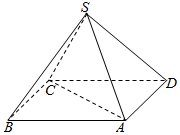 如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等
如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等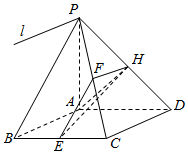 如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.