题目内容
15．在△ABC中，已知a=20，b=28，A=40°，求B（精确到1°）．分析 利用正弦定理计算求出sinB，得出B．
解答 解：由正弦定理得：$\frac{a}{sinA}=\frac{b}{sinB}$，
∴sinB=$\frac{bsinA}{a}$=$\frac{7sin40°}{5}$≈0.9
∴B=arcsin0.9≈64°或B=180°-64°=116°．
点评 本题考查了正弦定理，属于基础题．
练习册系列答案
相关题目
7．已知双曲线E的渐近线方程为3x±4y=0，且E的右焦点为（5，0），过双曲线E中心的直线与双曲线E交于A，B两点，在双曲线E上取一点C，直线AC，BC的斜率分别为k1、k2，则k1k2等于（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{9}{16}$ | D． | $\frac{16}{25}$ |
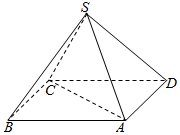如图，某人打算做一个正四棱锥形的金字塔模型，先用木料搭边框，再用其他材料填充．已知金字塔的每一条棱和边都相等