题目内容
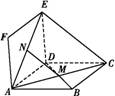
如图所示,在三棱锥P ABQ中,PB⊥平面ABQ,BA=BP=BQ,D、C、E、F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
ABQ中,PB⊥平面ABQ,BA=BP=BQ,D、C、E、F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
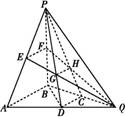
(1)求证:AB∥GH;
(2)求二面角D GH
GH E的余弦值.
E的余弦值.
(1)证明:由D、C、E、F分别是AQ,BQ,AP,BP的中点,知G,H分别是△PAQ,△PBQ的重心.
∴ =
= =
= .
.
∴GH∥DC.
又D,C为AQ,BQ的中点,则DC∥AB,
∴AB∥GH.
(2)解:在△ABQ中,

AQ=2BD,AD=DQ,
所以∠ABQ=90°,即AB⊥BQ,
因为PB⊥平面ABQ,
所以AB⊥PB.
又BP∩BQ=B,
所以AB⊥平面PBQ.
由(1)知AB∥GH,所以GH⊥平面PBQ.
又FH⊂平面PBQ,所以GH⊥FH.
同理可得GH⊥HC,
所以∠FHC为二面角D GH
GH E的平面角.
E的平面角.
设BA=BQ=BP=2,连接FC,
在Rt△FBC中,由勾股定理得FC= ,
,
在Rt△PBC中,由勾股定理得PC= .
.
又H为△PBQ的重心,
所以HC= PC=
PC= .同理FH=
.同理FH= .
.
在△FHC中,由余弦定理得
cos∠FHC= =
= =-
=- .
.
即二面角D GH
GH E的余弦值为-
E的余弦值为- .
.

练习册系列答案
相关题目
 A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是 (填出所有可能的序号).
A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是 (填出所有可能的序号). 

 A1B1C1D1的棱长为a,点M在AC1上且
A1B1C1D1的棱长为a,点M在AC1上且 =
= ,N为B1B的中点,则|
,N为B1B的中点,则|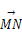 |为( )
|为( ) a (B)
a (B) a (C)
a (C) a (D)
a (D) a
a
 +
+ =1,则使得a+b≥μ恒成立的μ的取值范围是________.
=1,则使得a+b≥μ恒成立的μ的取值范围是________.