题目内容
直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
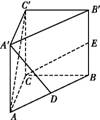
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
解:令 =a,
=a, =b,
=b, =c,
=c,
根据题意,|a|=|b|=|c|,
且a·b=b·c=c·a=0,
(1)∵ =b+
=b+ c,
c, =-c+
=-c+ b-
b- a.
a.
∴ ·
· =-
=- c2+
c2+ b2=0.
b2=0.
∴ ⊥
⊥ ,
,
即CE⊥A′D.
(2)∵ =-a+c,|
=-a+c,| |=
|=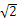 |a|,|
|a|,| |=
|= |a|.
|a|.
 ·
· =(-a+c)·(b+
=(-a+c)·(b+ c)=
c)= c2=
c2= |a|2,
|a|2,
∴cos< ,
, >=
>= =
= .
.
即异面直线CE与AC′所成角的余弦值为 .
.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目

 ABQ中,PB⊥平面ABQ,BA=BP=BQ,D、C、E、F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
ABQ中,PB⊥平面ABQ,BA=BP=BQ,D、C、E、F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.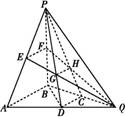
 (B)
(B) (C)
(C) (D)
(D)
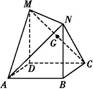
 AB
AB ,M、N分别是AC、BC的中点,则EM、AN所成角的余弦值等于 .
,M、N分别是AC、BC的中点,则EM、AN所成角的余弦值等于 . 
 ,
,