题目内容
11.已知函数f(x)的定义域是R,f′(x)是f(x)的导数,f(1)=e,g(x)=f′(x)-f(x),g(1)=0,g(x)的导数恒大于零,函数h(x)=f(x)-ex(e=2.71828…)是自然对数的底数)的最小值是0.分析 根据条件判断f′(x)与f(x)的关系,构造函数求出函数的最值,进行比较即可.
解答 解:∵f(1)=e,g(x)=f′(x)-f(x),g(1)=0,
∴g(1)=f′(1)-f(1)=0,则f′(1)=f(1)=e,
g′(x)>0恒成立,
即g(x)为增函数,
则当x>1时,g(x)>g(1)=0,
即f′(x)-f(x)>0,
当x<1时,g(x)<g(1)=0,
即f′(x)-f(x)<0,
构造函数m(x)=$\frac{f(x)}{{e}^{x}}$,
则m′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
则当x>1时,m′(x)>0,此时递增,
当x<1时,m′(x)<0,此时递减,
即函数m(x)取得极小值同时也是最小值m(1)=$\frac{f(1)}{e}$=1
即m(x)=$\frac{f(x)}{{e}^{x}}$≥1,
则f(x)≥ex,
则h(x)=f(x)-ex≥ex-ex=0,
即h(x)的最小值为0.
故答案为:0
点评 本题主要考查函数最值的应用,根据导数之间的关系,利用构造法是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
19.已知函数f(x)=xα,当x∈(1,+∞)时,f(x)-x<0,则( )
| A. | 0<α<1 | B. | α<1 | C. | α>0 | D. | α<0 |
16.对于R上可导的任意函数f(x),若满足f(x)=f(2-x),且(x-1)f′(x)≥0,则必有( )
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
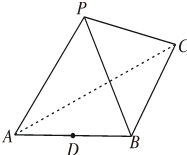 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.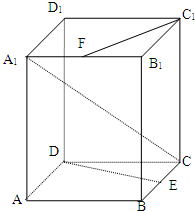 已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点.
已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点. 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.