题目内容
已知函数y=f(x)是定义在区间(-2,2)上的减函数,若f(m-1)>f(1-2m),则m的取值范围是 .
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据函数的单调性,得出不等式组,解出即可.
解答:
解:由题意得:
,解得:-
<m<
,
故答案为:(-
,
).
|
| 1 |
| 2 |
| 2 |
| 3 |
故答案为:(-
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查了函数的单调性,函数的定义域问题,是一道基础题.

练习册系列答案
相关题目
已知f(x)是R上的奇函数,g(x)是R上的偶函数,且f(x)+g(x)=ex,则“a+b>0”是“f(a)+g(b)>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
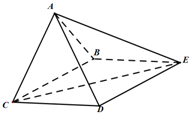 四棱锥A-ABCD中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
四棱锥A-ABCD中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=