题目内容
8.已知圆O:x2+y2=25,圆O1的圆心为O1(m,0),⊙O与⊙O1交于点P(3,4),过点P且斜率为k(k≠0)的直线l分别交⊙O、⊙O1于点A,B.(1)若k=1且$|BP|=7\sqrt{2}$,求⊙O1的方程;
(2)过点P作垂直于l的直线l1分别交⊙O、⊙O1于点C,D,当m为常数时,试判断|AB|2+|CD|2是否为定值?若是,求出这个定值;若不是,请说明理由.
分析 (1)通过k=1且$|BP|=7\sqrt{2}$,利用圆心到直线的距离与半径半弦长的关系,求出m的值,然后求圆O1的方程;
(2)设出A、B、C、D四点坐标,设出直线AB方程,通过方程组求出x1,x2,利用弦长公式求出AB,CD然后求出它们的和,即可判断是否是定值.
解答 解:(1)k=1时,直线l的方程为x-y+1=0,
由$|BP|=7\sqrt{2}$,得${(\frac{|m+1|}{{\sqrt{2}}})^2}+{(\frac{{7\sqrt{2}}}{2})^2}={(m-3)^2}+{4^2}$,解得m=14或m=0
因为m>0,所以m=14
即圆O1的方程为(x-14)2+y2=137;
(2)直线l的方程为y-4=k(x-3)
由$\left\{\begin{array}{l}{x^2}+{y^2}=25\\ y-4=k(x-3)\end{array}\right.$消去y得:(1+k2)x2+(8k-6k2)x+9k2-24k-9=0,
${x_B}+{x_A}=-\frac{{8k-6{k^2}}}{{1+{k^2}}}$,${x_B}{x_A}=\frac{{9{k^2}-24k-9}}{{1+{k^2}}}$,
$|AB{|^2}={({x_B}-{x_A})^2}+{({y_B}-{y_A})^2}$=$(1+{k^2}){({x_B}-{x_A})^2}$=$(1+{k^2})[{({x_B}+{x_A})^2}-4{x_B}{x_A}]=\frac{{4{m^2}}}{{1+{k^2}}}$,
因为直线l1垂直于l,所以用$-\frac{1}{k}$替换上式中的k,
得$|CD{|^2}=\frac{{4{m^2}}}{{1+{{(-\frac{1}{k})}^2}}}=\frac{{4{m^2}{k^2}}}{{1+{k^2}}}$,
所以|AB|2+|CD|2=4m2.
点评 本题考查圆的方程的求法,直线与圆的位置关系,弦长公式的应用,考查计算能力,转化思想.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | |a+b|≥a-b | B. | $2\sqrt{ab}≤|{a+b}|$ | C. | |a+b|<|a|+|b| | D. | $|{\frac{b}{a}+\frac{a}{b}}|≥2$ |

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
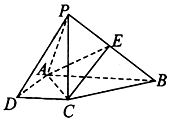 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点. 三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.
三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.