题目内容
7.在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是BB1,CC1的中点.(1)求证:AD∥平面A1EFD1;
(2)求直线AD到平面A1EFD1的距离.
分析 (1)利用线面平行的判定证明;
(2)过A作AH⊥A1E与H,JAH交A1E于G,则AH⊥面A1EFD1,
线段AG的长是直线AD到平面A1EFD1的距离,△AA1H∽△AGA1,则有$\frac{AG}{A{A}_{1}}=\frac{A{A}_{1}}{AH}$⇒AG即可.
解答 解:(1)证明:如图,∵E,F分别是BB1,CC1的中点,∴EF∥A1D1,∴四点A1、E、F、D1共面.
∵AD∥EF,AD?面A1EFD1,EF?A1EFD1∴AD∥平面A1EFD1
(2)正方体ABCD-A1B1C1D1中面 AA1B1B中⊥面A1EFD1.
过A作AH⊥A1E与H,JAH交A1E于G,则AH⊥面A1EFD1,
线段AG的长是直线AD到平面A1EFD1的距离,
△AA1H∽△AGA1,则有$\frac{AG}{A{A}_{1}}=\frac{A{A}_{1}}{AH}$⇒AG=$\frac{2\sqrt{5}}{5}a$
∴直线AD到平面A1EFD1的距离为$\frac{{2\sqrt{5}}}{5}a$.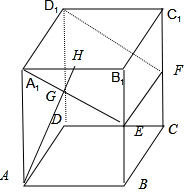
点评 本题考查了空间线面平行的判定,线面距离,属于中档题.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.若集合$A=\left\{{y\left|{y={x^{\frac{1}{3}}}}\right.}\right\},B=\left\{{x\left|{y=ln({x-1})}\right.}\right\}$,则A∩B=( )
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
15.已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则$\frac{2{S}_{n}+16}{{a}_{n}+3}$的最小值为( )
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | 2 |
16.若a,b∈R,则复数(a2-6a+10)+(-b2+4b-5)i对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知a,b∈R,ab>0,则下列不等式中不正确的是( )
| A. | |a+b|≥a-b | B. | $2\sqrt{ab}≤|{a+b}|$ | C. | |a+b|<|a|+|b| | D. | $|{\frac{b}{a}+\frac{a}{b}}|≥2$ |
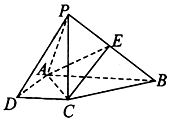 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.