题目内容

3位男生和3位女生共6位同学站成一排，若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同排法的种数是
 
种．（用数字作答）
考点：计数原理的应用
专题：排列组合
分析：先考虑3位女生中有且只有两位相邻的排列，减去在3女生中有且仅有两位相邻且男生甲在两端的排列．
解答： 解：先考虑3位女生中有且只有两位相邻的排列
共有C32A22A42A33=432种，
在3女生中有且仅有两位相邻且男生甲在两端的排列有2×C32A22A32A22=144种，
∴不同的排列方法共有432-144=288种
故答案为：288．
点评：本题考查排列组合及简单的计数原理，本题解题的关键是在计算时要做到不重不漏，把不合题意的去掉．
练习册系列答案
相关题目
设O为坐标原点，C为圆x2-4x+y2-1=0的圆心，且圆上有一点M（x，y）满足
OM
•
CM
=0，则
y
x
等于
 
．
在△ABC中，a，b，c分别是角A，B，C的对边，且a：b：c=
3
：1：2，则∠B为
 
．
若f（x）是定义在R上的偶函数，则f（1+
2
）-f（
1
1-
2
）=
 
．
求函数f（x）=x3-2f′（1）x在x=2处的切线方程
 
．
给出以下四个命题，其中所有正确命题的序号为：
 
．
（1）“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件；
（2）已知线性回归方程
∧
y
=3+2x，当变量x增加2个单位，其预报值
∧
y
平均增加4个单位；
（3）函数f（x）=ex-（
1
2
）x在区间（-1，1）上只有1个零点；
（4）命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2=0”；
（5）设随机变量ξ服从正态分布N（2，9），若P（ξ＞c+1）=P（ξ＜c-1），则c等于3．
若复数z满足iz=2+4i，则在复平面内，z的共轭复数
.
z
对应的点的坐标是（　　）
A、（2，4）
B、（2，-4）
C、（4，-2）
D、（4，2）
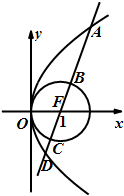已知抛物线y2=4x，圆F：（x-1）2+y2=1，过点F作直线l，自上而下顺次与上述两曲线交于点A，B，C，D（如图所示），则|AB|•|CD|的值正确的是（　　）
A、等于1B、最小值是1
C、等于4D、最大值是4
函数y=sin（-2x+
π
3
）在区间[0，π]上的单调递增区间为（　　）
A、[
5π
12
，
11π
12
]
B、[0，
5π
12
]
C、[
π
6
，
2π
3
]
D、[
2π
3
，π]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网