题目内容
3.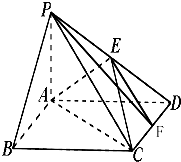 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.(1)当点F为DC的中点时,求证:EF∥平面PAC
(2)求证:无论点F在DC的何处,都有PF⊥AE
(3)求二面角E-AC-D的余弦值.
分析 (1)欲证EF∥平面PAC,根据直线与平面平行的判定定理可知只需证EF与平面PAC内一直线平行,根据中位线定理可知EF∥PC,PC?平面PAC,EF?平面PAC,满足定理所需条件;
(2)欲证PF⊥AE,而PF?平面PDC,可先证AE⊥平面PDC,根据CD⊥平面PAD,有线面垂直的性质可知AE⊥CD,根据等腰三角形可知AE⊥PD,CD∩PD=D,满足线面垂直的判定定理.
(3)过E坐EM⊥AD垂足为M,过M作MN⊥AC,垂足为N,连接EN.则∠MNE为二面角E-AC-D的平面角,在Rt△MNE中计算即可.
解答 解:(1)证明:当点F为CD的中点时,∵点E,F分别为CD,PD的中点,∴EF∥PC.(3分)
∵PC?平面PAC,EF?平面PAC,
∴EF∥平面PAC.
(2)证明:∵PA⊥平面ABCD,CD?平面ABCD,
∴CD⊥PA.又ABCD是矩形,∴CD⊥AD,
∵PA∩AD=A,∴CD⊥平面PAD.
∵AE?平面PAD,∴AE⊥CD.
∵PA=AD,点F是PD的中点,∴AE⊥PD.又CD∩PD=D,∴AE⊥平面PDC.
∵PF?平面PDC,∴PF⊥AE.
(3)过E坐EM⊥AD垂足为M,过M作MN⊥AC,垂足为N,连接EN.
易证∠MNE为二面角E-AC-D的平面角.
△ACD的边AC上的高为$\frac{1×\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$,∴MN=,$\frac{\sqrt{3}}{4}$,
∵EM=$\frac{1}{2}$,EN=$\sqrt{M{N}^{2}+E{M}^{2}}=\frac{\sqrt{7}}{4}$,
∴cos∠MNE=$\frac{\sqrt{7}}{4}$,
所以二面角E-AC-D的余弦值为$\frac{\sqrt{21}}{7}$.
点评 本题主要考查了直线与平面的判定,以及线面垂直的判定和性质等有关知识,同时考查了空间想象能力和推理论证的能力,二面角等知识,属于中档题.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方式从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交实验,选取的植株均为矮茎的概率是多少?
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,则判断框内的正整数
,则判断框内的正整数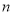 的值为( )
的值为( )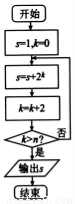
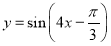 的图像,只需要将函数
的图像,只需要将函数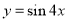 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移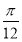 个单位
个单位 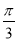 个单位 D.向右平移
个单位 D.向右平移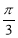 个单位
个单位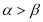 ,则
,则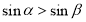 ;
;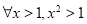 ”的否定是“
”的否定是“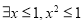 ”;
”;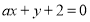 与
与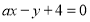 垂直的充要条件为
垂直的充要条件为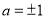 ;
; ,则
,则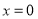 或
或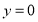 ”的逆否命题为“若
”的逆否命题为“若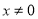 或
或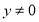 ,则
,则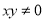 ”
”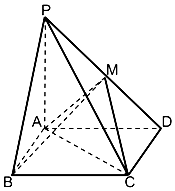 如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M. 如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.
如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.