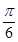题目内容
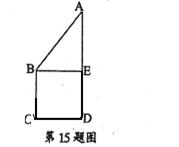
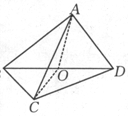
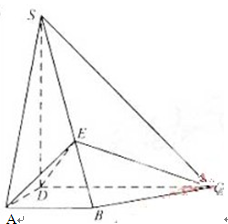
如图所示,已知正方形ABCD的边长为2,AC∩BD=O,将正方形ABCD沿对角线BD折起,得到三棱锥A—BCD。
(1)求证:平面AOC⊥平面BCD;
(2)若三棱锥A—BCD的体积为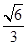 ,求AC的长。
,求AC的长。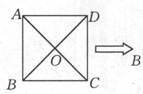
(1)求证:平面AOC⊥平面BCD;
(2)若三棱锥A—BCD的体积为
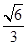 ,求AC的长。
,求AC的长。

(1)证明:因为
 是正方形,
是正方形,所以
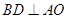 ,
,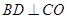 .…………………………1分
.…………………………1分在折叠后的△
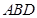 和△
和△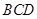 中,
中,仍有
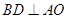 ,
,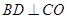 .…………………………2分
.…………………………2分因为
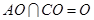 ,所以
,所以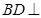 平面
平面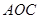 .………3分
.………3分因为
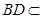 平面
平面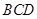 ,
,所以平面
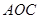
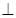 平面
平面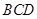 .…………………………4分
.…………………………4分 (2)解:设三棱锥
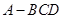 的高为
的高为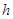 ,
,由于三棱锥
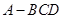 的体积为
的体积为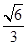 ,
,所以
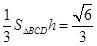 .因为
.因为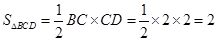 ,所以
,所以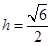 .…5分
.…5分
以下分两种情形求
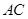 的长:
的长:①当
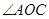 为钝角时,如图,过点
为钝角时,如图,过点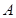 作
作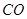 的垂线交
的垂线交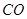 的延长线于点
的延长线于点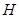 ,
,由(1)知
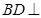 平面
平面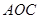 ,所以
,所以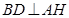 .
.又
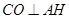 ,且
,且 ,所以
,所以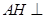 平面
平面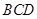 .
.所以
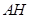 为三棱锥
为三棱锥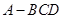 的高,即
的高,即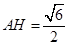 .………………………………………6分
.………………………………………6分在
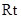 △
△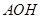 中,因为
中,因为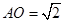 ,
,所以
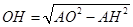
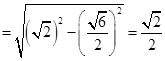 .………………7分
.………………7分在
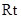 △
△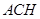 中,因为
中,因为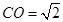 ,
,则
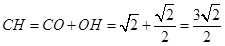 .…………………………8分
.…………………………8分所以
 .…………………………9分
.…………………………9分②当
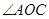 为锐角时,如图,过点
为锐角时,如图,过点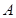 作
作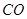 的垂线交
的垂线交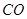 于点
于点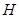 ,
,由(1)知
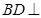 平面
平面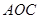 ,所以
,所以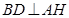 .
.又
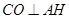 ,且
,且 ,所以
,所以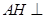 平面
平面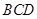 .
.所以
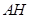 为三棱锥
为三棱锥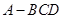 的高,即
的高,即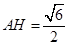 .
.在
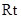 △
△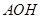 中,因为
中,因为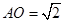 ,
,所以
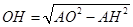
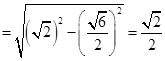 .…………10分
.…………10分在
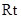 △
△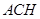 中,因为
中,因为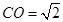 ,
,则
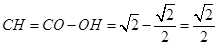 .
.所以
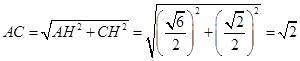 .…………………11分
.…………………11分综上可知,
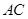 的长为
的长为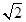 或
或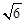 .
.
本试题主要是考查立体几何中垂直的证明,以及利用线面的垂直的判定定理和性质定理求解三棱锥的体积,得到AC的长度。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
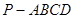 中,
中,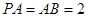 .
.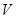 ;
;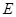 为侧棱
为侧棱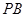 的中点,求异面直线
的中点,求异面直线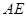 与
与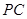
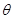 的大小.
的大小.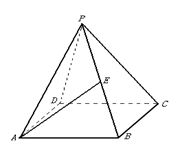
 ,
, 是两个不重合的平面,在下列条件中,可以判断
是两个不重合的平面,在下列条件中,可以判断 的是( )
的是( ) .
.
 为异面直线且
为异面直线且
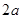 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C AB
AB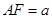 ,G是EF的中点,
,G是EF的中点,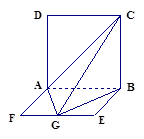
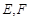 分别为BC,CD的中点,
分别为BC,CD的中点,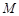 、
、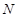 分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥
分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥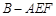 ,如图所示.
,如图所示.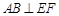 ;
;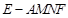 的体积.
的体积.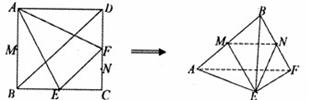
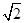 BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述: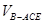 的体积是
的体积是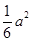 ;
;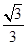 。
。