题目内容
求证：如果一条直线垂直于两个平面，那么这两个平面平行．
考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：先写出已知、求证，由面面平行的性质定理找到两组平行的相交直线，利用面面平行的第二判定定理可得结论．
解答：
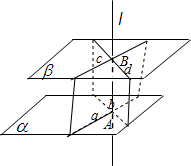已知：l⊥β，l⊥α，求证：α∥β．
证明：令平面γ与平面α、β分别相交于直线a，c，
由l⊥β，l⊥α，可得l⊥a，l⊥b，
又由a，c?γ，故a∥c，
再取与γ相交的另一个平面λ与平面α、β分别相交于直线b，d，
同理可得b∥d，
由a，b?α，c，d?β，
a∩b=B
∴α∥β．
已知：l⊥β，l⊥α，求证：α∥β．证明：令平面γ与平面α、β分别相交于直线a，c，
由l⊥β，l⊥α，可得l⊥a，l⊥b，
又由a，c?γ，故a∥c，
再取与γ相交的另一个平面λ与平面α、β分别相交于直线b，d，
同理可得b∥d，
由a，b?α，c，d?β，
a∩b=B
∴α∥β．
点评：本题考查线面垂直的性质，考查面面平行的判定判定，正确运用面面平行的第二判定定理，面面平行定理是关键．
练习册系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AA1=3，底面边长为
如图所示，已知四棱锥P-ABCD的底面是菱形，∠DAB=