题目内容
18.若偶函数f(x)在[1,2]上为增函数,且有最小值0,则它在[-2,-1]上( )| A. | 是减函数,有最小值0 | B. | 是增函数,有最小值0 | ||
| C. | 是减函数,有最大值0 | D. | 是增函数,有最大值0 |
分析 根据偶函数在关于原点对称的区间上单调性相反,可知f(x)在区间1,2]上的单调性,再由所给最小值为0,可求f(x)在[-2,-1]上的最值.
解答 解:因为f(x)在[1,2]上为增函数,且有最小值0,所以f(1)=0,
又f(x)为偶函数,所以f(x)在[-2,-1]上单调递减,f(x)≥f(-1)=f(1)=0.
即f(x)在区间[-2,-1]上的最小值为0,
综上,f(x)在区间[-2,-1]上单调递减,且最小值为0.
故选:A.
点评 本题考查函数的奇偶性、单调性及其应用,属基础题.

练习册系列答案
相关题目
13.已知函数f(x)=$\frac{1}{{\sqrt{3-x}}}$的定义域为M,g(x)=$\sqrt{x+1}$的定义域为N,则M∩N=( )
| A. | {x|x≥-1} | B. | {x|x<3} | C. | {x|-1<x<3} | D. | {x|-1≤x<3} |
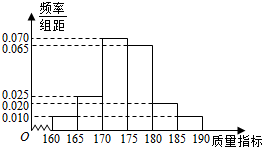 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.