题目内容
若向量
，
是两个互相垂直的单位向量，则向量
-
在向量
方向上的投影为 ．
| a |
| b |
| a |
| 3 |
| b |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先求得|
-
|的值，数形结合可得向量
-
和向量
的夹角为150°，根据
-
在向量
方向上的投影为|
-
|•cos150°，计算求得结果．
| a |
| 3 |
| b |
| a |
| 3 |
| b |
| b |
| a |
| 3 |
| b |
| b |
| a |
| 3 |
| b |
解答：
解：∵向量
，
是两个互相垂直的单位向量，∴
•
=0，
∴|
-
|=
=
=2．
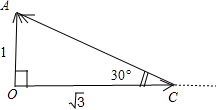
如图所示：设
=
，
=
，
=
-
，
显然，向量
-
和向量
的夹角为150°，
故
-
在向量
方向上的投影为 2•cos150°=-
．
故答案为：-
．
解：∵向量| a |
| b |
| a |
| b |
∴|
| a |
| 3 |
| b |
(
|
| 1+3-0 |
如图所示：设
| OA |
| a |
| OC |
| 3 |
| b |
| CA |
| a |
| 3 |
| b |
显然，向量
| a |
| 3 |
| b |
| b |
故
| a |
| 3 |
| b |
| b |
| 3 |
故答案为：-
| 3 |
点评：本题考查向量的投影，转化为向量的数量积和模长来运算是解决问题的关键，属于中档题．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、若p∨q为真命题，则p、q均为真命题． |
| C、命题“存在x∈R，使得x2+x+1＜0”的否定是：“对任意x∈R，均有x2+x+1＜0” |
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |