题目内容
 如图所示,在△ABC中,AB=AC=3,BC=2,B的平分线交过点A且与BC平行的线交于点D,求△ABD的面积.
如图所示,在△ABC中,AB=AC=3,BC=2,B的平分线交过点A且与BC平行的线交于点D,求△ABD的面积.考点:相似三角形的性质
专题:选作题,立体几何
分析:先求出S△ABC,再利用角平分线的性质,及相似三角形的性质,即可得出结论.
解答:
 解:作AM⊥BC于点M,则∵AB=AC,
解:作AM⊥BC于点M,则∵AB=AC,
∴BM=CM=1,
根据勾股定理AM=2
,
∴S△ABC=
•2•2
=2
,
∵BD是B的平分线,
∴S△ABE=
,S△CBE=
,
∵B的平分线交过点A且与BC平行的线交于点D,
∴S△ADE=
,
∴S△ABD=
+
=
.
 解:作AM⊥BC于点M,则∵AB=AC,
解:作AM⊥BC于点M,则∵AB=AC,∴BM=CM=1,
根据勾股定理AM=2
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
∵BD是B的平分线,
∴S△ABE=
6
| ||
| 5 |
4
| ||
| 5 |
∵B的平分线交过点A且与BC平行的线交于点D,
∴S△ADE=
6
| ||
| 5 |
∴S△ABD=
6
| ||
| 5 |
6
| ||
| 5 |
12
| ||
| 5 |
点评:本题考查角平分线的性质,及相似三角形的性质,考查学生的计算能力,比较基础.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
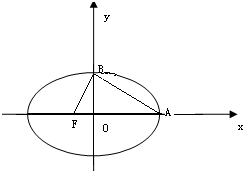 已知双曲线的中心在坐标原点,焦点在x轴上,A是右顶点,B是虚轴的上端点,F是左焦点,当BF⊥AB时,此类双曲线称为“黄金双曲线”,其离心率为e=
已知双曲线的中心在坐标原点,焦点在x轴上,A是右顶点,B是虚轴的上端点,F是左焦点,当BF⊥AB时,此类双曲线称为“黄金双曲线”,其离心率为e=