题目内容
2.下列四个结论中正确的个数为( )①命题“若x2<1,则-1<x<1”的逆否命题是“若x>1或x<-1,则x2>1”
②已知p:任意x∈R,sinx≤1,q:若am2<bm2,则a<b,p且q为真命题
③命题“存在x∈R,x2-x>0”的否定是“任意x∈R,x2-x≤0”;
④“x>2”是“x2>4”的必要不充分条件.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据逆否命题的定义进行判断.
②根据复合命题的真假关系进行判断.
③根据含有量词的命题的否定进行判断.
④根据充分条件和必要条件的定义进行判断.
解答 解:①命题“若x2<1,则-1<x<1”的逆否命题是“若x≥1或x≤-1,则x2≥1”故①错误,
②已知p:任意x∈R,sinx≤1,则p为真命题,q:若am2<bm2,则m≠0,则a<b,即q是真命题,则p且q为真命题,故②正确,
③命题“存在x∈R,x2-x>0”的否定是“任意x∈R,x2-x≤0”;正确,故③正确,
④由x2>4得x>2或x<-2,即“x>2”是“x2>4”的充分不必要条件.故④错误,
故正确的是②④,
故选:C.
点评 本题主要考查命题的真假判断,涉及四种命题真假关系,含有量词的命题的否定以及充分条件和必要条件的判断,综合性较强,但难度不大.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
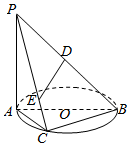 如图,AB是圆O的直径,点C是半圆的中点,PA⊥平面ABC,PA=AB,PB=6D是PB的中点,E是PC上一点.
如图,AB是圆O的直径,点C是半圆的中点,PA⊥平面ABC,PA=AB,PB=6D是PB的中点,E是PC上一点.
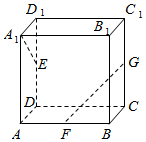 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,F为PC的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,F为PC的中点,PA=2AB=2.