题目内容
5.已知二次函数f(x)的图象与x轴的两个交点的距离是2,对称轴是x=-2,最小值是-1,这个二次函数的解析式是f(x)=x2+4x+3.分析 求出函数的图象和x轴的交点,设出函数的表达式,根据待定系数法求出函数的解析式即可.
解答 解:二次函数f(x)的图象与x轴的两个交点的距离是2,对称轴是x=-2,
∴图象和x轴的交点是(-3,0),(-1,0),
顶点坐标是(-2,-1),
设函数的解析式是f(x)=a(x-x1)(x-x2)=a(x+3)(x+1),
将(-2,-1)代入f(x)得:a=1,
∴f(x)=x2+4x+3,
故答案为:f(x)=x2+4x+3.
点评 本题考查了求函数的解析式问题,考查二次函数的性质,是一道基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.根据如下样本数据
求得y关于x的线性回归直线方程为$\widehat{y}$=2.1x+0.85,则m的值为0.5.
| x | 0 | 1 | 4m | 3 |
| y | m | 3 | m+5 | 7 |
16.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且a=1,b=2,c=$\sqrt{7}$,则∠C=( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
13.下列式子恒成立的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α-β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαsinβ-sinαcosβ |
17.已知向量$\overrightarrow{{A}{B}}$、$\overrightarrow{{A}C}$、$\overrightarrow{{A}D}$满足$\overrightarrow{{A}C}=\overrightarrow{{A}{B}}+\overrightarrow{{A}D}$,$|{\overrightarrow{{A}{B}}}|=2$,$|{\overrightarrow{{A}D}}|=1$,E、F分别是线段BC、CD的中点.若$\overrightarrow{D{E}}•\overrightarrow{{B}F}=-\frac{5}{4}$,则向量$\overrightarrow{{A}{B}}$与向量$\overrightarrow{{A}D}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
14.cos420°+sin330°等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
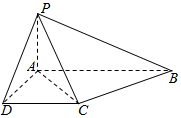 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: