题目内容
1.椭圆$\frac{x^2}{5}+\frac{y^2}{4}=1$的焦距是( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
分析 根据题意,由椭圆的标准方程可得a、b的值,计算可得c的值,进而由焦距定义计算可得答案.
解答 解:根据题意,椭圆的标准方程为:$\frac{x^2}{5}+\frac{y^2}{4}=1$,
则a2=5,b2=4,
则c=$\sqrt{{a}^{2}-{b}^{2}}$=1,
则其焦距2c=2;
故选:D.
点评 本题考查椭圆的几何性质,关键是掌握椭圆的标准方程的形式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
7.函数f(x)的导函数f′(x)的图象如图所示,则( )
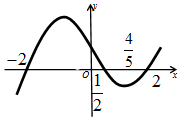

| A. | $\frac{1}{2}$为f(x)的极大值点 | B. | -2为f(x)的极大值点 | ||
| C. | 2为f(x)的极大值 | D. | $\frac{4}{5}$为f(x)的极小值点 |
13.设点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右支上,双曲线的左、右焦点分别为F1,F2,若|PF1|=4|PF2|,则双曲线离心率的取值范围是( )
| A. | $({1,\frac{5}{3}}]$ | B. | (1,2] | C. | $[{\frac{5}{3},+∞})$ | D. | [2,+∞) |
11.设f(x)=|sinπx|,则f(1)+f(2)+f(3)+…+f(2010)=( )
| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 1 |
 在三棱锥E一ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC.
在三棱锥E一ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC.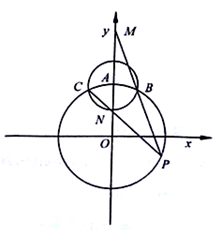 如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点.
如图,在平面直角坐标系xOy中,圆O:x2+y2=4与y轴的正半轴交于点A,以A为圆心的圆x2+(y-2)2=r2(r>0)与圆O交于B、C两点. 三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,
三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,