题目内容
已知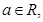 矩阵
矩阵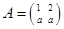 对应的线性变换把点
对应的线性变换把点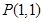 变成点
变成点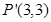 ,求矩阵
,求矩阵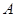 的特征值以及属于没个特征值的一个特征向量.
的特征值以及属于没个特征值的一个特征向量.
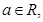 矩阵
矩阵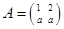 对应的线性变换把点
对应的线性变换把点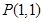 变成点
变成点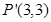 ,求矩阵
,求矩阵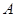 的特征值以及属于没个特征值的一个特征向量.
的特征值以及属于没个特征值的一个特征向量. =
= 是矩阵
是矩阵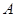 的属于特征值
的属于特征值 的一个特征向量
的一个特征向量解本题的突破口是由 ,得
,得 ,从而可得矩阵
,从而可得矩阵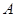 的特征多项式为
的特征多项式为 ,再令
,再令 ,得矩阵
,得矩阵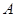 的特征值
的特征值 ,到此问题基本得以解决.
,到此问题基本得以解决.
解:由 ,得
,得
矩阵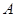 的特征多项式为
的特征多项式为
令 ,得矩阵
,得矩阵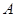 的特征值
的特征值
对于特征值 ,解相应的线性方程组
,解相应的线性方程组 得一个非零解
得一个非零解
因此, =
= 是矩阵
是矩阵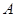 的属于特征值
的属于特征值 的一个特征向量 …………13分
的一个特征向量 …………13分
注:写出的特征向量只要满足 ,
, 即可
即可
 ,得
,得 ,从而可得矩阵
,从而可得矩阵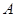 的特征多项式为
的特征多项式为 ,再令
,再令 ,得矩阵
,得矩阵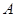 的特征值
的特征值 ,到此问题基本得以解决.
,到此问题基本得以解决.解:由
 ,得
,得
矩阵
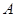 的特征多项式为
的特征多项式为
令
 ,得矩阵
,得矩阵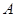 的特征值
的特征值
对于特征值
 ,解相应的线性方程组
,解相应的线性方程组 得一个非零解
得一个非零解
因此,
 =
= 是矩阵
是矩阵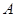 的属于特征值
的属于特征值 的一个特征向量 …………13分
的一个特征向量 …………13分注:写出的特征向量只要满足
 ,
, 即可
即可
练习册系列答案
相关题目
 的方程组:
的方程组:
 ,并对解的情况进行讨论.
,并对解的情况进行讨论. ,A的一个特征值
,A的一个特征值 ,属于λ的特征向量是
,属于λ的特征向量是 ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵. 满足
满足 ,则
,则 ,矩阵B=
,矩阵B= ,计算:AB= .
,计算:AB= .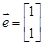 ,并且矩阵
,并且矩阵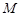 对应的变换将点
对应的变换将点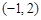 变成点
变成点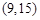 ,求出矩阵
,求出矩阵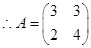 ,向量
,向量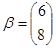 ,
,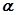 ,使得
,使得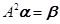 .
. ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )
个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )



 中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( )
中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( )