题目内容
选修4-2:矩阵与变换 已知矩阵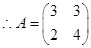 ,向量
,向量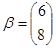 ,
,
(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量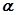 ,使得
,使得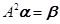 .
.
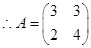 ,向量
,向量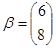 ,
,(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量
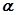 ,使得
,使得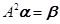 .
.(Ⅰ)由 得
得
 ,
,
当 时,求得对应的特征向量为
时,求得对应的特征向量为 ,
,
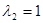 时,求得对应的特征向量为
时,求得对应的特征向量为 ;
;
(Ⅱ)设向量 ,由
,由 得
得 .
.
 得
得
 ,
,当
 时,求得对应的特征向量为
时,求得对应的特征向量为 ,
,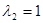 时,求得对应的特征向量为
时,求得对应的特征向量为 ;
; (Ⅱ)设向量
 ,由
,由 得
得 .
. 本试题主要是考查而来矩阵与变换的综合运用。矩阵的特征值和对应的特征向量,以及跟木向量与矩阵的关系得到向量的求解的综合运用。
(1)因为由 ,那么可以解得参数
,那么可以解得参数 的值。并且讨论得到对应的特征向量
的值。并且讨论得到对应的特征向量
(2)设向量 ,由矩阵的运算可知
,由矩阵的运算可知 ,从而解得
,从而解得
解:(Ⅰ)由 得
得
 ,
,
当 时,求得对应的特征向量为
时,求得对应的特征向量为 ,
,
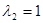 时,求得对应的特征向量为
时,求得对应的特征向量为 ;………………………4分
;………………………4分
(Ⅱ)设向量 ,由
,由 得
得 .………………7分
.………………7分
(1)因为由
 ,那么可以解得参数
,那么可以解得参数 的值。并且讨论得到对应的特征向量
的值。并且讨论得到对应的特征向量(2)设向量
 ,由矩阵的运算可知
,由矩阵的运算可知 ,从而解得
,从而解得
解:(Ⅰ)由
 得
得
 ,
,当
 时,求得对应的特征向量为
时,求得对应的特征向量为 ,
,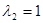 时,求得对应的特征向量为
时,求得对应的特征向量为 ;………………………4分
;………………………4分(Ⅱ)设向量
 ,由
,由 得
得 .………………7分
.………………7分
练习册系列答案
相关题目
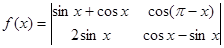 的最小正周期
的最小正周期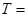
 ,若函数
,若函数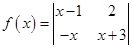 在
在 上单调递减,则实数
上单调递减,则实数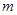 的取值范围是( )
的取值范围是( )



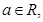 矩阵
矩阵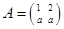 对应的线性变换把点
对应的线性变换把点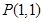 变成点
变成点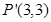 ,求矩阵
,求矩阵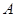 的特征值以及属于没个特征值的一个特征向量.
的特征值以及属于没个特征值的一个特征向量.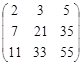
 B
B  C
C 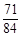 D
D 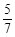
 的逆矩阵为 .
的逆矩阵为 .  在矩阵
在矩阵

 对应变换的作用下得到的点为
对应变换的作用下得到的点为
 ,求矩阵
,求矩阵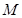 的逆矩阵.
的逆矩阵.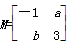 所对应的变换把直线l:2x-y=3变换为自身,
所对应的变换把直线l:2x-y=3变换为自身,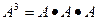 ,若矩阵
,若矩阵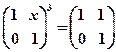 ,则
,则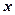 的值是_____________.
的值是_____________.