题目内容
19.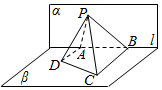 如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )
如图,已知平面α∩平面β=l,α⊥β.A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,DA=4,AB=6,CB=8.P是平面α上的一动点,且有∠APD=∠BPC,则四棱锥P-ABCD体积的最大值是( )| A. | 48 | B. | 16 | C. | $24\sqrt{3}$ | D. | 144 |
分析 由面面垂直的性质可得AD⊥PA,BC⊥PB,由∠APD=∠BPC可知PB=2PA,在平面α内建立坐标系求出P点的轨迹,得出P到直线l的最大距离,得出棱锥的最大体积.
解答 解:∵平面α∩平面β=l,α⊥β,DA⊥l,CB⊥l,DA?平面β,CB?平面β,
∴DA⊥平面α,CB⊥平面α,
∵PA?平面α,PB?平面α,
∴DA⊥PA,CB⊥PB.
∵∠APD=∠BPC,
∴$\frac{DA}{PA}=\frac{BC}{PB}$,即$\frac{4}{PA}=\frac{8}{PB}$,∴PB=2PA.
以直线l为x轴,AB的中点为坐标原点建立平面直角坐标系,
则A(-3,0),B(3,0).设P(x,y),则PA=$\sqrt{(x+3)^{2}+{y}^{2}}$,PB=$\sqrt{(x-3)^{2}+{y}^{2}}$,
∴2$\sqrt{(x+3)^{2}+{y}^{2}}$=$\sqrt{(x-3)^{2}+{y}^{2}}$,整理得(x+5)2+y2=16(y>0).
∴P点的轨迹为以(-5,0)为圆心,以4为半径的半圆.
∴当P到直线l的距离h=4时,四棱锥P-ABCD体积取得最大值.
∴棱锥的体积最大值为V=$\frac{1}{3}{S}_{梯形ABCD}•h$=$\frac{1}{3}×\frac{1}{2}×(4+8)×6×4$=48.
故选:A.
点评 本题考查了面面垂直的性质,轨迹方程,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
9.若中心在原点,对称轴为坐标轴的双曲线的渐近线方程为y=±$\sqrt{2}$x,则该双曲线的离心率为( )
| A. | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{6}}{2}$或3 | C. | $\sqrt{3}$ | D. | 3 |
10.已知双曲线的离心率e=$\frac{5}{3}$,点(0,5)为其一个焦点,则该双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 |
4.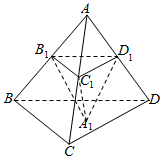 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )| A. | 当x=$\frac{2}{3}$时,函数f(x)取到最大值 | |
| B. | 函数f(x)在($\frac{1}{2}$,1)上是减函数 | |
| C. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| D. | 存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$(其中VA-BCD为四面体ABCD的体积) |
9.某火锅店为了了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:
(Ⅰ)求y关于x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(Ⅱ)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
(Ⅱ)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
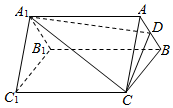 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.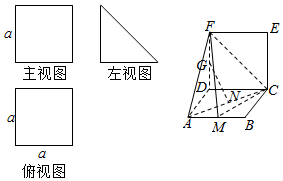 一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个棱柱的直观图和三视图(主视图和俯视图是边长为a的正方形,左视图是直角边长为a的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点. 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,侧棱OB⊥底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.