题目内容
【题目】已知数列{an}中，a1=1，an+1=
，（n∈N*）
（1）求数列{an}的通项公式an，
（2）若数列{bn}满足bn=（3n﹣1）
an，数列{bn}的前n项和为Tn，若不等式（﹣1）nλ＜Tn对一切n∈N*恒成立，求λ的取值范围．
【答案】（1）an=
．（2）﹣1＜λ＜2．
【解析】
试题（1）由已知条件推导出
，从而得到
=（
）3n﹣1=
．由此能求出结果．
（2）由
=
，利用裂项求和法求出
，从而得到{Tn}为单调递增数列，由此利用分类讨论思想能求出λ的取值范围．
解：（1）∵数列{an}中，a1=1，an+1=
，（n∈N*）
∴
=
，
∴
，
∴
=（
）3n﹣1=
．
∴an=．
（2）∵
，bn=（3n﹣1）
an，
∴
=
，
∴
，①
，②
①﹣②，得
=
﹣
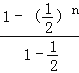=2﹣
，
∴
．，
∵Tn+1﹣Tn=（4﹣
）﹣（4﹣
）=
，
∴{Tn}为单调递增数列，
∵不等式（﹣1）nλ＜Tn对一切n∈N*恒成立，
∴①当n为正奇数时，﹣λ＜Tn对一切正奇数成立，
∴（Tn）min=T1=1，∴﹣λ＜1，∴λ＞﹣1；
②当n为正偶数时，λ＜Tn对一切正偶数成立，
∵（Tn）min=T2=2，∴λ＜2．
综上知﹣1＜λ＜2．
练习册系列答案
相关题目
