Question

【题目】如图，已知三棱锥D－ABC中，二面角A－BC－D的大小为90°，且∠BDC＝90°，∠ABC＝30°，BC＝3，．

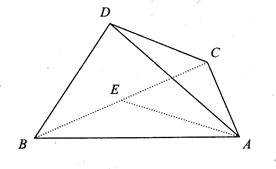
（1）求证：AC⊥平面BCD；

（2）二面角B－AC－D为45°，且E为线段BC的中点，求直线AE与平面ACD所成的角的正弦值．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1））△ABC中,根据条件利用余弦定理求出AC,根据勾股定理证明垂直即可（2）以C为原点，CB所在直线为x轴，CA所在直线为y轴，过点C作垂直于平面ABC的直线为z轴建立空间直角坐标系，求出平面ACD的法向量，利用直线与平面所成角公式计算即可.

（1）△ABC中，由，

解得，从而AC2+BC2＝AB2，∴AC⊥BC；又二面角A-BC-D的大小为90°，即平面BCD⊥平面ABC，

而平面BCD∩平面ABC＝BC，AC平面ABC，故AC⊥平面BCD；

（2）以C为原点，CB所在直线为x轴，CA所在直线为y轴，过点C作垂直于平面ABC的直线为z轴，建立如图所示的空间直角坐标系，

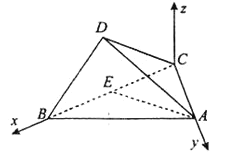
故平面ABC的法向量＝(0，0，1)，

设平面ACD的法向量＝(1，m，n)，由，易知m＝0，

从而＝(1，0，n)，，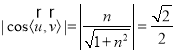

解得n＝±1，结合实际图形，可知n取1时，二面角为135°，应舍去，

所以＝(1，0，-1)，

易知，B(3，0，0)，故，则，

设直线AE与平面ACD所成的角为θ，

则，即直线AE与平面ABC所成的角的正弦值为．