题目内容
10.直线x+2y=m(m>0)与⊙O:x2+y2=5交于A,B两点,若$|{\overrightarrow{OA}+\overrightarrow{OB}}|>2|{\overrightarrow{AB}}|$,则m的取值范围为(2$\sqrt{5}$,5).分析 根据直线与圆有两个交点可推断出圆心到直线的距离小于或等于半径,根据$|{\overrightarrow{OA}+\overrightarrow{OB}}|>2|{\overrightarrow{AB}}|$,利用平行四边形法则推断出∠AOB范围,通过夹角为直角时求得原点到直线的距离,可得d范围,求得m的范围.
解答 解:∵直线x+2y+m=0与圆x2+y2=5交于相异两点A、B,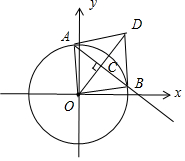
∴O点到直线x+2y+m=0的距离d<$\sqrt{5}$,
又∵|$\overrightarrow{OA}$+$\overrightarrow{OB}$|>2|$\overrightarrow{AB}$|,由OADB是菱形,并且OC>2AC,
可知,OC>2.
圆的圆心到直线的距离d>2,
可得:$\sqrt{5}$>$\frac{m}{\sqrt{5}}$>2,m>0,解得m∈(2$\sqrt{5}$,5).
故答案为:(2$\sqrt{5}$,5).
点评 本题主要考查了直线与圆相交的性质,向量的几何意义等.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
16.已知随机变量ξ服从正态分布N(1,σ2).若P(0<ξ≤1)=0.4,则P(ξ≥2)=( )
| A. | 0.4 | B. | 0.3 | C. | 0.2 | D. | 0.1 |
18.已知数列{an}的通项${a_n}={2^n}cos({nπ})$,则a1+a2+…+a100=( )
| A. | 0 | B. | $\frac{{2-{2^{101}}}}{3}$ | C. | 2-2101 | D. | $\frac{2}{3}({{2^{100}}-1})$ |
5.已知三棱锥P-A BC四个顶点都在半径为2的球面上,PA⊥面ABC,PA=2,底面ABC是正三角形,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
| A. | $\frac{7π}{4}$ | B. | 2π | C. | $\frac{9π}{4}$ | D. | 3π |
15.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A. | y=ln|x| | B. | y=-x2+1 | C. | y=$\frac{1}{x}$ | D. | y=cosx |
2.已知等差数列{an}中,a3+a11=50,a4=13,则数列{an}的公差等于( )
| A. | 1 | B. | 4 | C. | 5 | D. | 6 |
19.不等式|x-4|≤3的整数解的个数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.已知幂函数f(x)=xa的图象过点(4,2),令${a_n}=\frac{1}{f(n+1)+f(n)}$(n∈N*),记数列{an}的前n项和为Sn,则S2018=( )
| A. | $\sqrt{2018}+1$ | B. | $\sqrt{2018}-1$ | C. | $\sqrt{2019}+1$ | D. | $\sqrt{2019}-1$ |