题目内容
已知函数f(x)=
其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的最大值为( )
|
| A、-1 | B、-2 | C、-3 | D、-4 |
考点:分段函数的应用
专题:函数的性质及应用
分析:求函数的导数f′(x)=(x-a)(x-1),结合分段函数的表达式从而确定函数的单调性,利用基本不等式进行求解即可.
解答:
解:由分段函数可得f(0)=ka,
当x<0时,f′(x)=x2-(a+1)x+a=(x-1)(x-a),
若对任意的非零的实数x1,存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,
则知函数f(x)在(-∞,0)上是增函数,
当x≥0时,f(x)=k(x+a),此时对应直线和x轴的交点为(-a,0),
若a<0,则不满足函数f(x)在(-∞,0)上是增函数,
当a=0时,f(x)=
,此时不满足条件,
故a>0,
而由-a2-1=ka知,
k=
=-(a+
)≤-2
=-2,
(当且仅当a=
,即a=1时,等号成立);
故k的最大值为-2,
故选:B
当x<0时,f′(x)=x2-(a+1)x+a=(x-1)(x-a),
若对任意的非零的实数x1,存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,
则知函数f(x)在(-∞,0)上是增函数,
当x≥0时,f(x)=k(x+a),此时对应直线和x轴的交点为(-a,0),
若a<0,则不满足函数f(x)在(-∞,0)上是增函数,
当a=0时,f(x)=
|
故a>0,
而由-a2-1=ka知,
k=
| -a2-1 |
| a |
| 1 |
| a |
a•
|
(当且仅当a=
| 1 |
| a |
故k的最大值为-2,
故选:B
点评:本题主要考查分段函数的应用,利用导数研究函数的单调性是解决本题的关键.综合性较强,有一点的难度.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若函数f(x)的导函数是f′(x)=x2-4x+3,则函数g(x)=f(ax)(0<a<1)的单调递减区间是( )
| A、[loga3,0],[1,+∞) |
| B、(-∞,loga3],[0,+∞) |
| C、[a3,a] |
| D、[loga3,1] |
有10个乒乓球,将它们任意分成两堆,求出这两堆乒乓球个数的乘积,再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积,如此下去,直到不能再分为止,则所有乘积的和为( )
| A、45 | B、55 | C、90 | D、100 |
 如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
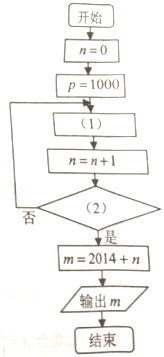 某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.
某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.