题目内容
17.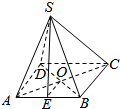 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
分析 连结AC、BD,交于点O,连结SO,由已知推导出∠SEO是正四棱锥的侧面SAB的斜高SE和底面AC所成角,由此能求出该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
解答  解:连结AC、BD,交于点O,连结SO,
解:连结AC、BD,交于点O,连结SO,
∵S-ABCD是正四棱锥,底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,
∴SO⊥底面ABCD,
∴∠SEO是正四棱锥的侧面SAB的斜高SE和底面AC所成角,
由题意得SE=$\sqrt{S{B}^{2}-B{E}^{2}}$=$\sqrt{45-9}$=6,
OE=$\frac{1}{2}AB=3$,
∴cos∠SEO=$\frac{OE}{SE}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴∠SEO=60°.
∴该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小为60°.
点评 本题考查线面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
7.对某电子元件进行寿命追踪调查,情况如下.
(1)画出频率分布直方图;
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
5.函数$y=\frac{1}{\sqrt{{-x}^{2}+2x+3}}$的单调减区间是( )
| A. | (1,3) | B. | (-∞,1) | C. | (-1,1) | D. | [-1,1] |
2.若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于( )
| A. | 120° | B. | 60° | C. | 30° | D. | 60°或30° |
6.在“①高一数学课本中的难题;②所有的正三角形; ③方程x2-4=0的实数解”中,能够表示成集合的是( )
| A. | ② | B. | ③ | C. | ②③ | D. | ①②③ |
 某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数).
某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数). 如图正方形ABCD的边长为ABCD的边长为$2\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,$FO=\sqrt{3},且FO⊥$平面ABCD.
如图正方形ABCD的边长为ABCD的边长为$2\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,$FO=\sqrt{3},且FO⊥$平面ABCD.