题目内容

6．在“①高一数学课本中的难题；②所有的正三角形； ③方程x2-4=0的实数解”中，能够表示成集合的是（　　）
A．②B．③C．②③D．①②③

分析 根据集合的定义，特别是集合中元素的“确定性”，分析可得结果．

解答 解：根据集合的定义，特别是集合中元素的“确定性”，分析如下：
①不能构成集合，因为“难题”无明确标准，元素不满足确定性；
②能构成集合，该集合可以写成{正三角形}或{x|x是正三角形}；
③能构成集合，该集合可以写成{-2，2}．
故选C．

点评 本题主要考查了集合的定义，以及集合中元素的性质，属于基础题．

练习册系列答案
相关题目
16．在△ABC中，∠ACB=90°，D为BC的中点，PA⊥平面ABC，如果PB，PC与平面ABC所成角分别为30°、60°，那么PD与平面ABC所成角的大小为45°．
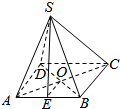17．如图，S-ABCD是正四棱锥，已知底面边长AB=6cm，侧棱SA=3$\sqrt{5}$cm，求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小．
14．如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．
（1）求异面直线BC与AE所成的角；
（2）求直线BE和平面ABC所成角的正弦值．
1．已知x=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$，y=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$，则3x2-5xy+3y2的值是289．
11．已知函数$f（x）=\left\{\begin{array}{l}{2^x}，x≤0\\ a{log_2}x，x＞0\end{array}\right.$，且f（-1）=f（2），则$f（{\frac{1}{4}}）$=-1．
18．已知平行四边形ABCD中，AB=6，AD=10，BD=8，E是线段AD的中点，沿直线BD将△BCD翻折成△BC′D，使得平面BC′D⊥平面ABD．
（Ⅰ）求证：平面DEC′⊥平面ABD；
（Ⅱ）求直线BD与平面BEC′所成角的正弦值．
15．一个圆锥的侧面展开图是圆心角为$\frac{4}{3}π$，半径为18的扇形，则这个圆锥的体积为$288\sqrt{5}π$．
16．已知命题p：x2-x-2＞0，q：|x|＜a，若￢p是q的必要而不充分条件，则实数a的取值范围是（　　）
A．a＜1B．a≤1C．a＜2D．a≤2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网