题目内容
5.函数$y=\frac{1}{\sqrt{{-x}^{2}+2x+3}}$的单调减区间是( )| A. | (1,3) | B. | (-∞,1) | C. | (-1,1) | D. | [-1,1] |
分析 先求出定义域,再结合复合函数的单调性规律可知$y=\frac{1}{\sqrt{{-x}^{2}+2x+3}}$的单调减区间即为y=-x2+2x+3在定义域内的增区间.
解答 解:由函数有意义得-x2+2x+3>0,解得-1<x<3.
又∵y=-x2+2x+3对称轴为x=1,
∴y=-x2+2x+3在(-1,1]单调递增,在(1,3)上单调递减,
∴$y=\frac{1}{\sqrt{{-x}^{2}+2x+3}}$的单调减区间是(-1,1).
故选:C.
点评 本题考查了复合函数的单调性,掌握复合函数的单调性规律是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
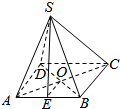 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.