题目内容
已知长方体ABCD-A1B1C1D1的外接球半径为4,则△AA1B,△ABD,△AA1D的面积之和的最大值为 .
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:设长方体长,宽,高分别为a,b,c.由已知可得长方体体对角线长为8,即a2+b2+c2=8,由柯西不等式公式有(a2+b2+c2)(1+1+1)≥(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,可得ab+bc+ac≤8,即可求出△AA1B,△ABD,△AA1D的面积之和的最大值.
解答:
解:设长方体长,宽,高分别为a,b,c.由已知可得长方体体对角线长为8,即a2+b2+c2=8,
由柯西不等式公式有(a2+b2+c2)(1+1+1)≥(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
即a2+b2+c2≥ab+bc+ac,即ab+bc+ac≤8,
又△AA1B,△ABD,△AA1D的面积之和为S=
(ab+bc+ac)≤4,
所以△AA1B,△ABD,△AA1D的面积之和的最大值为4.
由柯西不等式公式有(a2+b2+c2)(1+1+1)≥(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
即a2+b2+c2≥ab+bc+ac,即ab+bc+ac≤8,
又△AA1B,△ABD,△AA1D的面积之和为S=
| 1 |
| 2 |
所以△AA1B,△ABD,△AA1D的面积之和的最大值为4.
点评:本题考查求△AA1B,△ABD,△AA1D的面积之和的最大值,考查柯西不等式公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列叙述中正确的是( )
| A、若 p∧(¬q)为假,则一定是p假q真 |
| B、命题“?x∈R,x2≥0”的否定是“?x∈R,x2≥0” |
| C、若a,b,c∈R,则“ab2>cb2”的充分不必要条件是“a>c” |
| D、α是一平面,a,b是两条不同的直线,若 a⊥α,b⊥α,则a∥b |
已知等腰三角形底边的两个端点是A(-1,-1),B(3,7),则第三个顶点C的轨迹方程( )
| A、2x+y-7=0 |
| B、2x+y-7=0(x≠1) |
| C、x+2y-7=0 |
| D、x+2y-7=0(x≠1) |
函数f(x)=log2|2x-1|的图象大致是( )
A、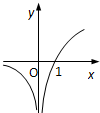 |
B、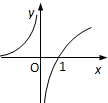 |
C、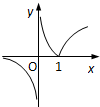 |
D、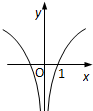 |