题目内容
20．一椭圆的两个焦点坐标分别为F1（0，-8），F2（0，8），且椭圆上的一点到两个焦点的距离之和为20，则此椭圆的标准方程为（ ）| A． | $\frac{x^2}{100}$+$\frac{y^2}{36}$=1 | B． | $\frac{y^2}{400}$+$\frac{x^2}{336}$=1 | C． | $\frac{y^2}{100}$+$\frac{x^2}{36}$=1 | D． | $\frac{y^2}{20}$+$\frac{x^2}{12}$=1 |
分析 由题意可设椭圆的标准方程为：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）．可得c=8，2a=20，b2=a2-c2，联立解出即可得出．
解答 解：由题意可设椭圆的标准方程为：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）．
则c=8，2a=20，b2=a2-c2，
联立解得a=10，b=6．
∴椭圆的标准方程为：$\frac{{y}^{2}}{100}$+$\frac{{x}^{2}}{36}$=1．
故选：C．
点评 本题考查了椭圆的定义、标准方程及其性质，考查了计算能力，属于基础题．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
8．已知等比数列{an}各项都为正数，且满足a2=2，a6=6，a4=（ ）
| A． | 4 | B． | 8 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
15．已知a＜0，函数f（x）=ax2+bx+c，若x0满足2ax+b=0，则下列必为真命题的是（ ）
| A． | ?x∈R，f（x）＞f（x0） | B． | ?x∈R，f（x-1）≥f（x0） | C． | ?x∈R，f（x）≤f（x0） | D． | ?x∈R，f（x+1）≥f（x0） |
5．已知{an}为等差数列，{bn}为正项等比数列，公比q≠1，若a1=b1，a13=b13，则（ ）
| A． | a7=b7 | B． | a7＞b7 | C． | a7＜b7 | D． | a7＞b7或a7＜b7 |
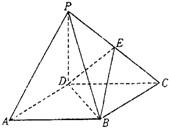如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．
9．两直线x-2y+7=0和2x+y-1=0的交点坐标为（ ）
| A． | （1，3） | B． | （-1，3） | C． | （3，-1） | D． | （-3，-1） |