题目内容
10．已知p：|m-$\frac{x-1}{3}}$|≤2；q：|x-2|+|x-3|＞3．若￢p是￢q的必要不充分条件．求实数m的取值范围．分析 分别求出p，q为真时的x的范围，根据￢p是￢q的必要不充分条件，得到P?Q，得到关于m的不等式，解出即可．
解答 解：p对应的集合为 P={x|3m-5≤x≤3m+7}，
q对应的集合为Q={x|x＜1或x＞4}，
因为?p是?q的必要不充分条件，
即?p??q，所以p⇒q，
所以P?Q，
所以3m+7＜1或3m-5＞4，
所以m＜-2或m＞3．
点评 本题考查了绝对值不等式问题，考查充分必要条件以及四种命题的关系，是一道基础题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
20．一椭圆的两个焦点坐标分别为F1（0，-8），F2（0，8），且椭圆上的一点到两个焦点的距离之和为20，则此椭圆的标准方程为（ ）
| A． | $\frac{x^2}{100}$+$\frac{y^2}{36}$=1 | B． | $\frac{y^2}{400}$+$\frac{x^2}{336}$=1 | C． | $\frac{y^2}{100}$+$\frac{x^2}{36}$=1 | D． | $\frac{y^2}{20}$+$\frac{x^2}{12}$=1 |
1．已知两个力$\overrightarrow{{F}_{1}}$，$\overrightarrow{{F}_{2}}$的夹角为90°，它们的合力大小为10N，合力与$\overrightarrow{{F}_{1}}$的夹角为60°，那么$\overrightarrow{{F}_{1}}$的大小为（ ）
| A． | 5$\sqrt{3}$N | B． | 5N | C． | 10N | D． | 5$\sqrt{2}$N |
5．已知α为锐角，且cos（α+$\frac{π}{12}}$）=$\frac{3}{5}$，则sin2α的值为（ ）
| A． | $\frac{{24-7\sqrt{3}}}{50}$ | B． | $\frac{{24+7\sqrt{3}}}{50}$ | C． | $\frac{{24\sqrt{3}-7}}{50}$ | D． | $\frac{{24\sqrt{3}+7}}{50}$ |
15．
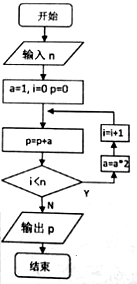要使如图所示的程序框图输出的P不小于60，则输入的n值至少为（ ）
要使如图所示的程序框图输出的P不小于60，则输入的n值至少为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 4 |