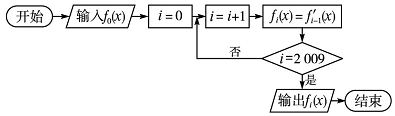
题目内容
2.在正方体ABCD-A1B1C1D1中,P为AA1中点,Q为CC1的中点,AB=2,则三棱锥B-PQD的体积为$\frac{4}{3}$.分析 由题意画出图形,取PQ中点G,连接BG,DG,可得PQ⊥平面BGD,求出△BDG的面积,代入棱锥体积公式求解.
解答 解:如图,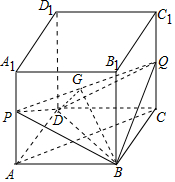
连接PQ,则PQ∥AC,取PQ中点G,连接BG,DG,
可得BG⊥PQ,DG⊥PQ,
又BG∩DG=G,则PQ⊥平面BGD,
在Rt△BPG中,由BP=$\sqrt{5}$,PG=$\sqrt{2}$,可得BG=$\sqrt{3}$,
同理可得DG=$\sqrt{3}$,则△BDG边BD上的高为$\sqrt{(\sqrt{3})^{2}-(\sqrt{2})^{2}}=1$,
∴${S}_{△BDG}=\frac{1}{2}×2\sqrt{2}×1=\sqrt{2}$,
则${V}_{B-PQD}=\frac{1}{3}×\sqrt{2}×2\sqrt{2}=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查柱、锥、台体积的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.复数z=1+3i的模等于( )
| A. | 2 | B. | 4 | C. | $\sqrt{10}$ | D. | $2\sqrt{2}$ |