题目内容
14.在如图所示框图中,输入f0(x)=cos x,则输出的是-sinx.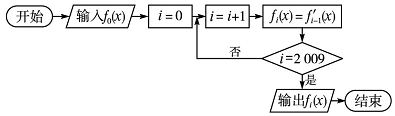
分析 根据框图的流程依次计算程序运行的结果,直到满足条件i=2009,程序运行终止,根据fn(x)的值是周期性变化规律求输出f2009(x)的值.
解答 解:由程序框图知:第一次运行i=0+1=1,f1(x)=f0′(x)=-sinx;
第二次运行i=1+1=2,f2(x)=-cosx;
第三次运行i=2+1=3,f3(x)=sinx;
第四次运行i=3+1=4,f4(x)=cosx;
第五次运行i=4+1=5,f5(x)=-sinx,
…
∴fn(x)的值是周期性变化的,且周期为4,
当i=2009时,满足条件i=2009,程序运行终止,输出f2009(x)=-sinx.
故答案为-sinx.
点评 本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.

练习册系列答案
相关题目
14.已知在△ABC中,内角A,B,C所对的边分别是a,b,c,若sin(B-A)+sin(B+A)=3sin2A,且c=$\sqrt{7}$,C=$\frac{π}{3}$,则△ABC的面积是( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{7\sqrt{3}}{6}$ | C. | $\frac{\sqrt{21}}{3}$ | D. | $\frac{3\sqrt{3}}{4}$或$\frac{7\sqrt{3}}{6}$ |
5.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x}+3,x≥0}\\{ax+b,x<0}\end{array}\right.$,满足条件:对于任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x1)=f(x2).当$f({\sqrt{3}a})=f({4b})$成立时,则实数a+b=( )
| A. | $-\sqrt{2}+3$ | B. | 5 | C. | $\sqrt{2}+3$ | D. | 1 |
6.某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |