题目内容
(本小题满分13分)设函数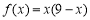 ,对于任意给定的
,对于任意给定的 位自然数
位自然数 (其中
(其中 是个位数字,
是个位数字, 是十位数字,
是十位数字, ),定义变换
),定义变换 :
: . 并规定
. 并规定 .记
.记 ,
,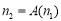 ,
, ,
,  ,
, .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)当 时,证明:对于任意的
时,证明:对于任意的 位自然数
位自然数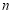 均有
均有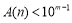 ;
;
(Ⅲ)如果 ,写出
,写出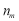 的所有可能取值.(只需写出结论)
的所有可能取值.(只需写出结论)
(Ⅰ) ; (Ⅱ)详见解析;(Ⅲ)详见解析
; (Ⅱ)详见解析;(Ⅲ)详见解析
【解析】
试题分析:(Ⅰ)由于 ,
, ,
, ,
, ,
, ,
, ,即可求出
,即可求出 .
.
(Ⅱ)因为函数 ,所以对于非负整数
,所以对于非负整数 ,知
,知 .(当
.(当 或5时,取到最大值),因为
或5时,取到最大值),因为  , 所以
, 所以  . 令
. 令  ,则
,则 .当
.当 时,
时, ,根据
,根据 的单调递增,即可求证结果;
的单调递增,即可求证结果;
(Ⅲ)根据(Ⅱ)即可得到结果.
试题解析:(Ⅰ)【解析】 ,
, ,
, ,
, ,
, ,
, ,
,
所以  . 3分
. 3分
(Ⅱ)证明:因为函数 ,
,
所以对于非负整数 ,知
,知 .(当
.(当 或5时,取到最大值) 4分
或5时,取到最大值) 4分
因为 ,
,
所以 . 6分
. 6分
令  ,则
,则 .
.
当 时,
时, ,
,
所以  ,函数
,函数 ,(
,( ,且
,且 )单调递增.
)单调递增.
故  ,即
,即 .
.
所以当 时,对于任意的
时,对于任意的 位自然数
位自然数 均有
均有 . 9分
. 9分
(Ⅲ)答: 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38. 14分.
的所有可能取值为0,8,14,16,20,22,26,28,32,36,38. 14分.
考点:1.归纳推理;2.单调性在不等式证明中的应用.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 中,已知
中,已知 ,则
,则 的值为______.
的值为______. 为双曲线C:
为双曲线C: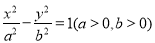 的左、右焦点,且直线
的左、右焦点,且直线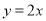 为双曲线C的一条渐近线,点P为C上一点,如果
为双曲线C的一条渐近线,点P为C上一点,如果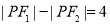 ,那么双曲线C的方程为____;离心率为_____.
,那么双曲线C的方程为____;离心率为_____.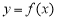 的定义域为
的定义域为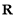 ,则“
,则“ ”是“函数
”是“函数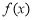 为奇函数”的( )
为奇函数”的( ) , x∈R的部分图象如图所示.
, x∈R的部分图象如图所示.
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 的值.
的值.  表示的平面区域,点
表示的平面区域,点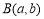 为坐标平面
为坐标平面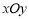 内一点,若对于区域D内的任一点
内一点,若对于区域D内的任一点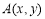 ,都有
,都有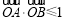 成立,则
成立,则 的最大值等于( )
的最大值等于( ) 在
在 是单调函数,则实数
是单调函数,则实数 的取值范围是 。
的取值范围是 。 的正三角形
的正三角形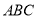 的边
的边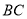 上有
上有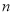 (
(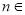 N*,
N*,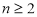 )等分点,沿向量
)等分点,沿向量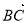 的方向依次为
的方向依次为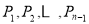 ,记
,记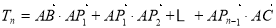 ,若给出四个数值:①
,若给出四个数值:①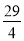 ②
②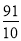 ③
③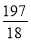 ④
④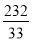 ,则
,则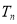 的值不可能的共有( )
的值不可能的共有( )