题目内容
(本小题满分13分)已知函数 , x∈R的部分图象如图所示.
, x∈R的部分图象如图所示.

(Ⅰ)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ) 设点B是图象上的最高点,点A是图象与x轴的交点,求 的值.
的值.
(Ⅰ) ,
, ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(Ⅰ)因为 =
= ,利用周期公式即可求出函数
,利用周期公式即可求出函数 的最小正周期;令
的最小正周期;令 ,即可求出函数
,即可求出函数 的单调递增区间;(Ⅱ)过点
的单调递增区间;(Ⅱ)过点 作线段
作线段 垂直于
垂直于 轴于点
轴于点
 ,由题意,得
,由题意,得 ,
, ,即可求出
,即可求出 的值.
的值.
试题解析:(Ⅰ)【解析】
因为
 2分
2分
= , 4分
, 4分
所以  .
.
故函数 的最小正周期为
的最小正周期为 . 6分
. 6分
由题意,得 ,解得
,解得 ,
,
所以函数 的单调递增区间为
的单调递增区间为 . 9分
. 9分
(Ⅱ)【解析】
如图过点 作线段
作线段 垂直于
垂直于 轴于点
轴于点 .
.

 由题意,得
由题意,得 ,
, ,
,
所以 . 13分.
. 13分.
考点:1.三角恒等变换;2.解三角形.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

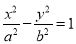 的虚轴长为2,焦距为
的虚轴长为2,焦距为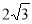 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).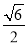 B.
B.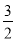 C.
C.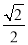 D.
D.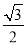
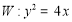 的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l:
的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l: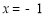 的距离为
的距离为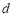 ,则有( )
,则有( )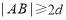 (B)
(B) (C)
(C)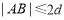 (D)
(D)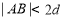
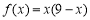 ,对于任意给定的
,对于任意给定的 位自然数
位自然数 (其中
(其中 是个位数字,
是个位数字, 是十位数字,
是十位数字, ),定义变换
),定义变换 :
: . 并规定
. 并规定 .记
.记 ,
,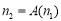 ,
, ,
, ,求
,求 ;
; 时,证明:对于任意的
时,证明:对于任意的 位自然数
位自然数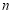 均有
均有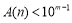 ;
; ,写出
,写出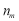 的所有可能取值.(只需写出结论)
的所有可能取值.(只需写出结论) 为双曲线C:
为双曲线C: 的左、右焦点,点P为双曲线C上一点,如果
的左、右焦点,点P为双曲线C上一点,如果 ,那么双曲线C的方程为____;离心率为____.
,那么双曲线C的方程为____;离心率为____.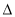 ABC中,角A,B,C所对的边分别为a,b,c. 若
ABC中,角A,B,C所对的边分别为a,b,c. 若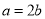 ,
,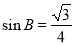 ,则( )
,则( )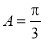 (B)
(B)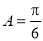
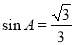 (D)
(D)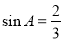
 ,若函数
,若函数 在区间
在区间 上有三个零点,则实数
上有三个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C.  D.
D.
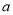 为大于
为大于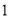 的常数,函数
的常数,函数 ,若关于
,若关于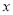 的方程
的方程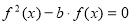 恰有三个不同的实数解,则实数
恰有三个不同的实数解,则实数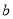 的取值范围是 .
的取值范围是 .