题目内容
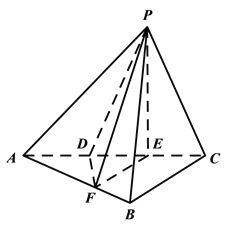
【题目】如图,三棱锥P-ABC中,平面PAC![]() 平面ABC,
平面ABC, ![]() ABC=
ABC=![]() ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB![]() 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
【答案】(1)见解析(2) BC=3或BC=3![]()
【解析】试题分析:(Ⅰ)先由已知易得![]() ,再注意平面
,再注意平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,再由线面垂直的性质可得到
,再由线面垂直的性质可得到![]() ,再注意到
,再注意到![]() ,而
,而![]() ,从而有
,从而有![]() ,那么由线面垂的判定定理可得
,那么由线面垂的判定定理可得![]() 平面
平面![]() ,
,
(Ⅱ)设![]() 则可用
则可用![]() 将四棱锥
将四棱锥![]() 的体积表示出来,由已知其体积等于7,从而得到关于
的体积表示出来,由已知其体积等于7,从而得到关于![]() 的一个一元方程,解此方程,再注意到
的一个一元方程,解此方程,再注意到![]() 即可得到
即可得到![]() 的长.
的长.
试题解析:证明:如题(20)图.由![]() 知,
知, ![]() 为等腰
为等腰![]() 中
中![]() 边的中点,故
边的中点,故
![]() ,
,
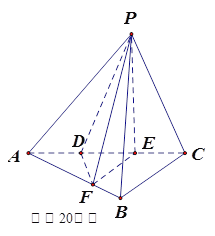
又平面![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,从而
,从而![]() .
.
因![]() .
.
从而![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() ,
, ![]() 都垂直,
都垂直,
所以![]() 平面
平面![]() .
.
(2)解:设![]() ,则在直角
,则在直角![]() 中,
中,
![]() .从而
.从而![]()
由![]() ,知
,知![]() ,得
,得![]() ,故
,故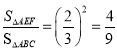 ,
,
即![]() .
.
由![]() ,
,![]() ,
,
从而四边形DFBC的面积为![]()
![]()
由(1)知,PE![]() 平面
平面![]() ,所以PE为四棱锥P-DFBC的高.
,所以PE为四棱锥P-DFBC的高.
在直角![]() 中,
中, ![]() ,
,
体积![]() ,
,
故得![]() ,解得
,解得![]() ,由于
,由于![]() ,可得
,可得![]() .
.
所以![]() 或
或![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目