Question

【题目】已知数列各项均为正数， ， ，且对任意恒成立，记的前项和为.

（1）若，求的值；

（2）证明：对任意正实数， 成等比数列；

（3）是否存在正实数，使得数列为等比数列.若存在，求出此时和的表达式；若不存在，说明理由.

Answer 1

【答案】（1）（2）见解析（3）存在使数列为等比数列，此时， .

【解析】试题分析：（1）根据， ，且对任意恒成立，代值计算即可．

（2）a1=1，a2=2，且anan+3=an+1an+2对任意n∈N*恒成立，则可得，从而的奇数项和偶数项均构成等比数列，即可证明，

（3）在（2）中令，则数列是首项为3，公比为的等比数列，从而得到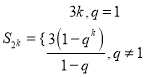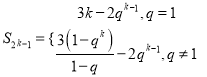， ．又数列为等比数列，解得，∴， ，∴求出此时和的表达式.

试题解析：

解：（1）∵，∴，又∵，∴；

（2）由，两式相乘得，

∵，∴，

从而的奇数项和偶数项均构成等比数列，

设公比分别为，则， ，

又∵，∴，即，

设，则，且恒成立，

数列是首项为，公比为的等比数列，问题得证；

（3）在（2）中令，则数列是首项为3，公比为的等比数列，

∴

，

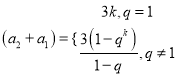
且， ， ， ，

∵数列为等比数列，∴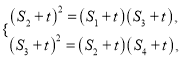

即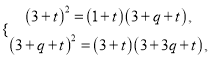即

解得（舍去），

∴， ，

从而对任意有，

此时， 为常数，满足成等比数列，

当时， ，又，∴，

综上，存在使数列为等比数列，此时， .